Question Number 136408 by nimnim last updated on 21/Mar/21
![S=Σ_(k=0) ^∞ ((3k^2 )/(2k^3 +2)) =? =Σ_(k=0) ^∞ (1/2)(((3k^2 )/(k^3 +1)))=Σ_(k=0) ^∞ (1/2)[(1/(k+1))+((2k−1)/(k^2 −k+1))] I dont know how to continue...Please Help.](https://www.tinkutara.com/question/Q136408.png)
$$\:\:\:\:\:\:{S}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{3}{k}^{\mathrm{2}} }{\mathrm{2}{k}^{\mathrm{3}} +\mathrm{2}}\:\:=? \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}{k}^{\mathrm{2}} }{{k}^{\mathrm{3}} +\mathrm{1}}\right)=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{k}+\mathrm{1}}+\frac{\mathrm{2}{k}−\mathrm{1}}{{k}^{\mathrm{2}} −{k}+\mathrm{1}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:{I}\:{dont}\:{know}\:{how}\:{to}\:{continue}…{Please}\:{Help}. \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 21/Mar/21
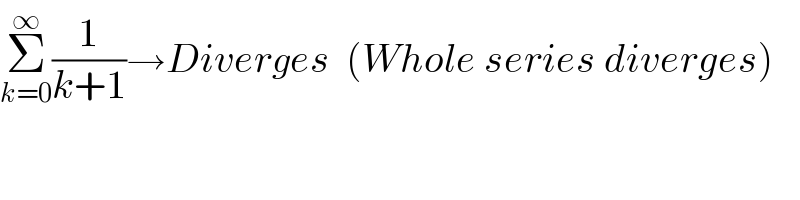
$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{1}}\rightarrow{Diverges}\:\:\left({Whole}\:{series}\:{diverges}\right) \\ $$
Commented by nimnim last updated on 21/Mar/21

$${Thank}\:{you}\:{sir}.. \\ $$
Answered by mathmax by abdo last updated on 21/Mar/21
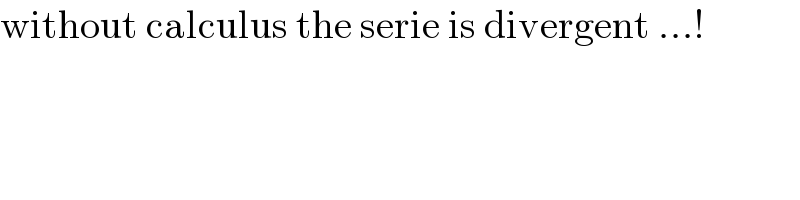
$$\mathrm{without}\:\mathrm{calculus}\:\mathrm{the}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{divergent}\:…! \\ $$
