S-n-2-k-2-n-1-n-n-1-S-

Question Number 7590 by FilupSmith last updated on 05/Sep/16

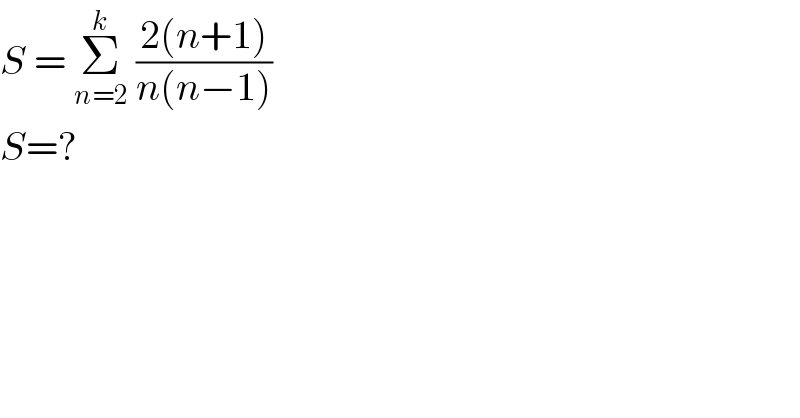
$${S}\:=\:\underset{{n}=\mathrm{2}} {\overset{{k}} {\sum}}\:\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}\left({n}−\mathrm{1}\right)} \\ $$$${S}=? \\ $$

Commented by Yozzia last updated on 05/Sep/16

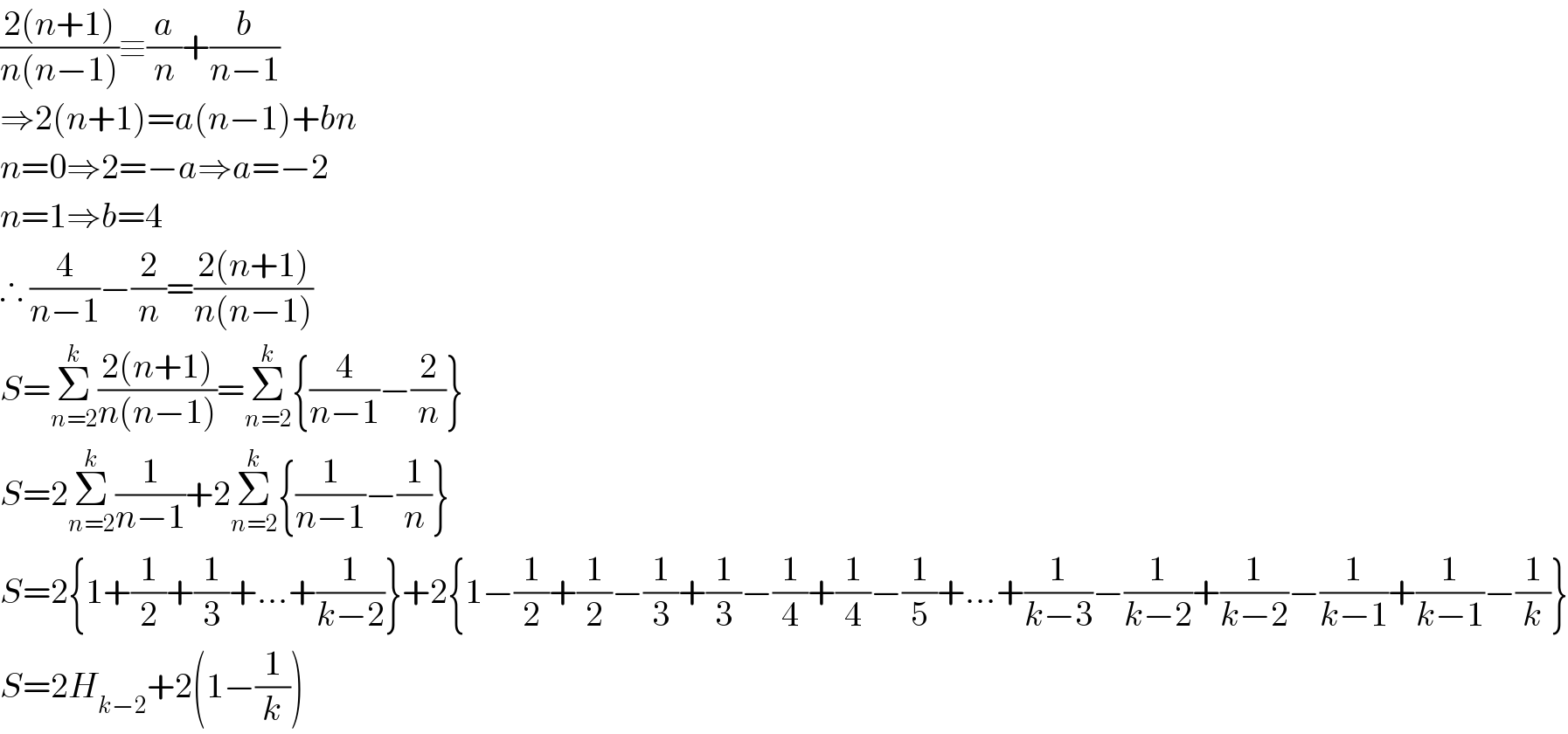
((2(n+1))/(n(n−1)))≡(a/n)+(b/(n−1)) ⇒2(n+1)=a(n−1)+bn n=0⇒2=−a⇒a=−2 n=1⇒b=4 ∴ (4/(n−1))−(2/n)=((2(n+1))/(n(n−1))) S=Σ_(n=2) ^k ((2(n+1))/(n(n−1)))=Σ_(n=2) ^k {(4/(n−1))−(2/n)} S=2Σ_(n=2) ^k (1/(n−1))+2Σ_(n=2) ^k {(1/(n−1))−(1/n)} S=2{1+(1/2)+(1/3)+...+(1/(k−2))}+2{1−(1/2)+(1/2)−(1/3)+(1/3)−(1/4)+(1/4)−(1/5)+...+(1/(k−3))−(1/(k−2))+(1/(k−2))−(1/(k−1))+(1/(k−1))−(1/k)} S=2H_(k−2) +2(1−(1/k))

$$\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}\left({n}−\mathrm{1}\right)}\equiv\frac{{a}}{{n}}+\frac{{b}}{{n}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}\left({n}+\mathrm{1}\right)={a}\left({n}−\mathrm{1}\right)+{bn} \\ $$$${n}=\mathrm{0}\Rightarrow\mathrm{2}=−{a}\Rightarrow{a}=−\mathrm{2} \\ $$$${n}=\mathrm{1}\Rightarrow{b}=\mathrm{4} \\ $$$$\therefore\:\frac{\mathrm{4}}{{n}−\mathrm{1}}−\frac{\mathrm{2}}{{n}}=\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}\left({n}−\mathrm{1}\right)} \\ $$$${S}=\underset{{n}=\mathrm{2}} {\overset{{k}} {\sum}}\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}\left({n}−\mathrm{1}\right)}=\underset{{n}=\mathrm{2}} {\overset{{k}} {\sum}}\left\{\frac{\mathrm{4}}{{n}−\mathrm{1}}−\frac{\mathrm{2}}{{n}}\right\} \\ $$$${S}=\mathrm{2}\underset{{n}=\mathrm{2}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{n}−\mathrm{1}}+\mathrm{2}\underset{{n}=\mathrm{2}} {\overset{{k}} {\sum}}\left\{\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}}\right\} \\ $$$${S}=\mathrm{2}\left\{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{{k}−\mathrm{2}}\right\}+\mathrm{2}\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{5}}+…+\frac{\mathrm{1}}{{k}−\mathrm{3}}−\frac{\mathrm{1}}{{k}−\mathrm{2}}+\frac{\mathrm{1}}{{k}−\mathrm{2}}−\frac{\mathrm{1}}{{k}−\mathrm{1}}+\frac{\mathrm{1}}{{k}−\mathrm{1}}−\frac{\mathrm{1}}{{k}}\right\} \\ $$$${S}=\mathrm{2}{H}_{{k}−\mathrm{2}} +\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{{k}}\right) \\ $$

Commented by FilupSmith last updated on 05/Sep/16

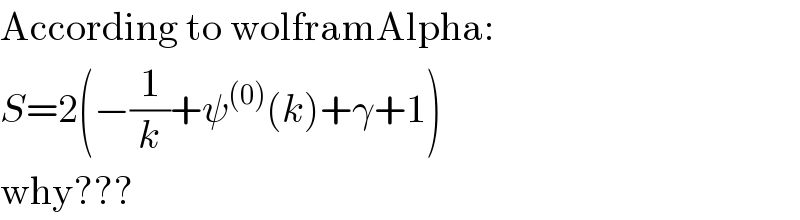
According to wolframAlpha: S=2(−(1/k)+ψ^((0)) (k)+γ+1) why???

$$\mathrm{According}\:\mathrm{to}\:\mathrm{wolframAlpha}: \\ $$$${S}=\mathrm{2}\left(−\frac{\mathrm{1}}{{k}}+\psi^{\left(\mathrm{0}\right)} \left({k}\right)+\gamma+\mathrm{1}\right) \\ $$$$\mathrm{why}??? \\ $$

Commented by FilupSmith last updated on 05/Sep/16

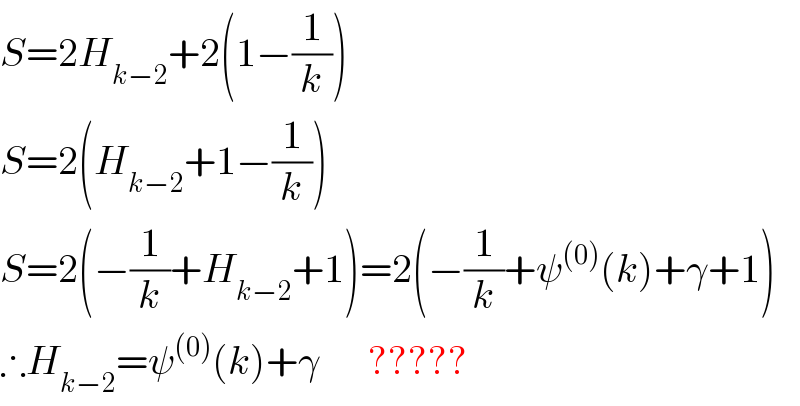
S=2H_(k−2) +2(1−(1/k)) S=2(H_(k−2) +1−(1/k)) S=2(−(1/k)+H_(k−2) +1)=2(−(1/k)+ψ^((0)) (k)+γ+1) ∴H_(k−2) =ψ^((0)) (k)+γ ?????

$${S}=\mathrm{2}{H}_{{k}−\mathrm{2}} +\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{{k}}\right) \\ $$$${S}=\mathrm{2}\left({H}_{{k}−\mathrm{2}} +\mathrm{1}−\frac{\mathrm{1}}{{k}}\right) \\ $$$${S}=\mathrm{2}\left(−\frac{\mathrm{1}}{{k}}+{H}_{{k}−\mathrm{2}} +\mathrm{1}\right)=\mathrm{2}\left(−\frac{\mathrm{1}}{{k}}+\psi^{\left(\mathrm{0}\right)} \left({k}\right)+\gamma+\mathrm{1}\right) \\ $$$$\therefore{H}_{{k}−\mathrm{2}} =\psi^{\left(\mathrm{0}\right)} \left({k}\right)+\gamma\:\:\:\:\:\:????? \\ $$

Commented by 123456 last updated on 05/Sep/16

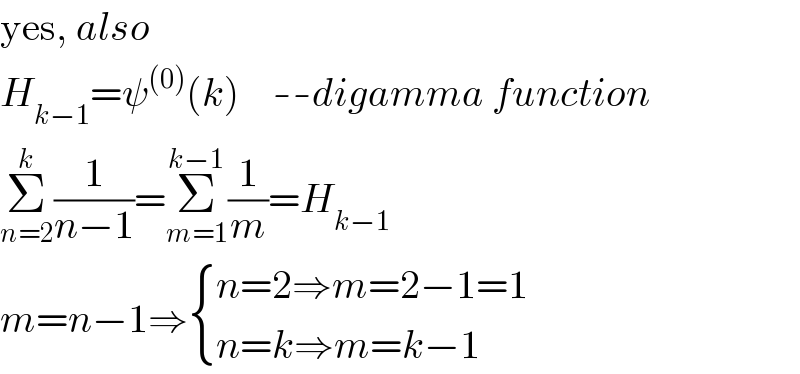
yes, also H_(k−1) =ψ^((0)) (k) --digamma function Σ_(n=2) ^k (1/(n−1))=Σ_(m=1) ^(k−1) (1/m)=H_(k−1) m=n−1⇒ { ((n=2⇒m=2−1=1)),((n=k⇒m=k−1)) :}

$$\mathrm{yes},\:{also} \\ $$$${H}_{{k}−\mathrm{1}} =\psi^{\left(\mathrm{0}\right)} \left({k}\right)\:\:\:\:–{digamma}\:{function} \\ $$$$\underset{{n}=\mathrm{2}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{n}−\mathrm{1}}=\underset{{m}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{{m}}={H}_{{k}−\mathrm{1}} \\ $$$${m}={n}−\mathrm{1}\Rightarrow\begin{cases}{{n}=\mathrm{2}\Rightarrow{m}=\mathrm{2}−\mathrm{1}=\mathrm{1}}\\{{n}={k}\Rightarrow{m}={k}−\mathrm{1}}\end{cases} \\ $$

Facebook Tweet Pin

S-n-2-k-2-n-1-n-n-1-S-

Leave a Reply Cancel reply