Menu Close

S-n-k-0-n-1-n-k-n-k-

Tinku Tara 0 Comments
Pin




Question Number 142023 by SOMEDAVONG last updated on 25/May/21
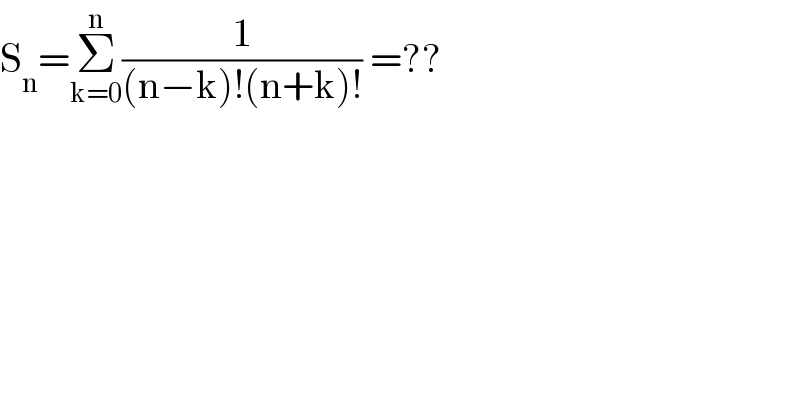
S_n =Σ_(k=0) ^n (1/((n−k)!(n+k)!)) =??
$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{k}\right)!\left(\mathrm{n}+\mathrm{k}\right)!}\:=?? \\ $$
Answered by aleks041103 last updated on 25/May/21
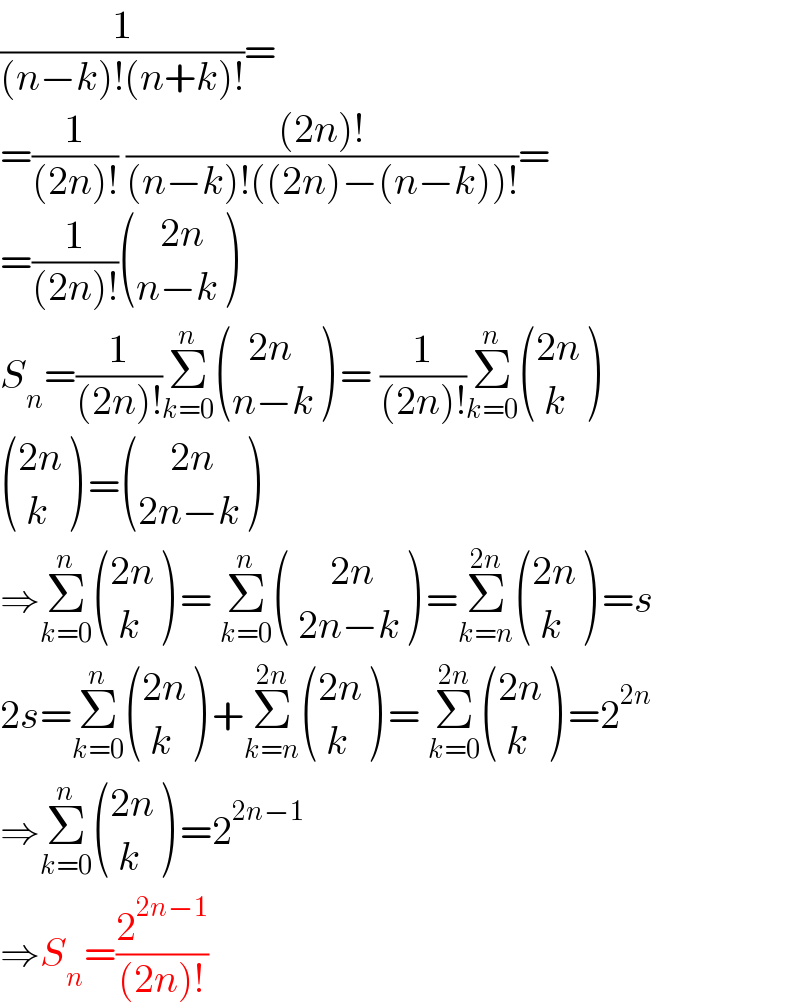
(1/((n−k)!(n+k)!))= =(1/((2n)!)) (((2n)!)/((n−k)!((2n)−(n−k))!))= =(1/((2n)!)) ((( 2n)),((n−k)) ) S_n =(1/((2n)!))Σ_(k=0) ^n ((( 2n)),((n−k)) ) = (1/((2n)!))Σ_(k=0) ^n (((2n)),(( k)) ) (((2n)),(( k)) ) = ((( 2n)),((2n−k)) ) ⇒Σ_(k=0) ^n (((2n)),(( k)) ) = Σ_(k=0) ^n ((( 2n)),(( 2n−k)) ) =Σ_(k=n) ^(2n) (((2n)),(( k)) ) =s 2s=Σ_(k=0) ^n (((2n)),(( k)) ) +Σ_(k=n) ^(2n) (((2n)),(( k)) ) = Σ_(k=0) ^(2n) (((2n)),(( k)) ) =2^(2n) ⇒Σ_(k=0) ^n (((2n)),(( k)) ) =2^(2n−1) ⇒S_n =(2^(2n−1) /((2n)!))
$$\frac{\mathrm{1}}{\left({n}−{k}\right)!\left({n}+{k}\right)!}= \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)!}\:\frac{\left(\mathrm{2}{n}\right)!}{\left({n}−{k}\right)!\left(\left(\mathrm{2}{n}\right)−\left({n}−{k}\right)\right)!}= \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)!}\begin{pmatrix}{\:\:\:\mathrm{2}{n}}\\{{n}−{k}}\end{pmatrix} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)!}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\:\:\mathrm{2}{n}}\\{{n}−{k}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)!}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix} \\ $$$$\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:=\begin{pmatrix}{\:\:\:\:\mathrm{2}{n}}\\{\mathrm{2}{n}−{k}}\end{pmatrix} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:=\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\:\:\:\:\:\mathrm{2}{n}}\\{\:\mathrm{2}{n}−{k}}\end{pmatrix}\:=\underset{{k}={n}} {\overset{\mathrm{2}{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:={s} \\ $$$$\mathrm{2}{s}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:+\underset{{k}={n}} {\overset{\mathrm{2}{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:=\mathrm{2}^{\mathrm{2}{n}} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{\mathrm{2}{n}}\\{\:{k}}\end{pmatrix}\:=\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} \\ $$$$\Rightarrow{S}_{{n}} =\frac{\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}\right)!} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *