S-n-t-k-2n-1-S-

Question Number 9532 by FilupSmith last updated on 14/Dec/16

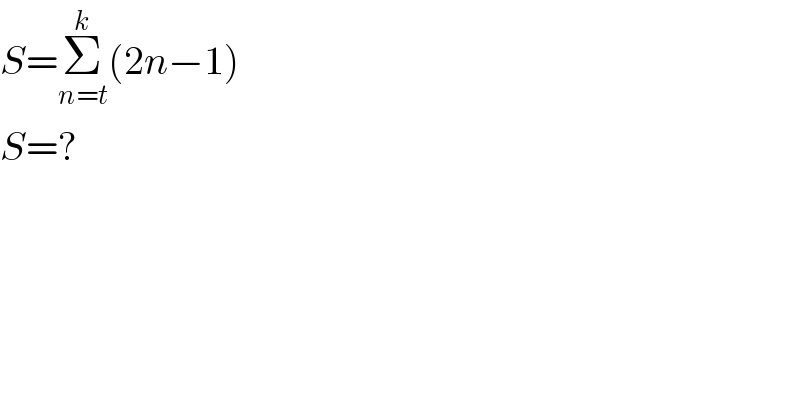
$${S}=\underset{{n}={t}} {\overset{{k}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$${S}=? \\ $$

Commented by sou1618 last updated on 14/Dec/16

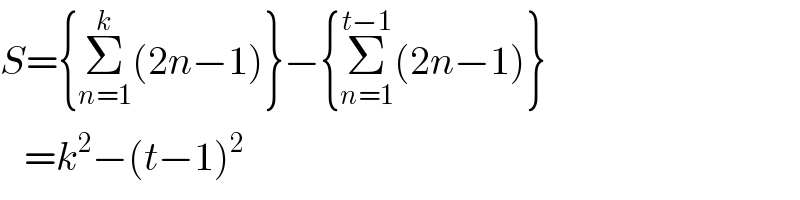
S={Σ_(n=1) ^k (2n−1)}−{Σ_(n=1) ^(t−1) (2n−1)} =k^2 −(t−1)^2

$${S}=\left\{\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right)\right\}−\left\{\underset{{n}=\mathrm{1}} {\overset{{t}−\mathrm{1}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right)\right\} \\ $$$$\:\:\:={k}^{\mathrm{2}} −\left({t}−\mathrm{1}\right)^{\mathrm{2}} \\ $$

Commented by FilupSmith last updated on 14/Dec/16

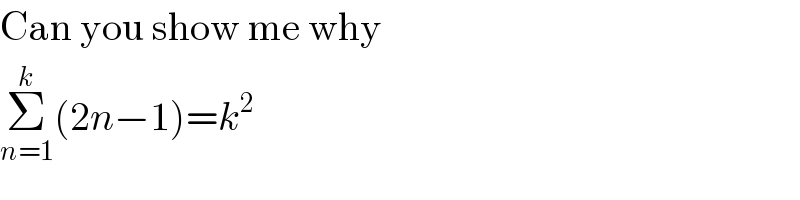
Can you show me why Σ_(n=1) ^k (2n−1)=k^2

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{me}\:\mathrm{why} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right)={k}^{\mathrm{2}} \\ $$

Commented by sou1618 last updated on 14/Dec/16

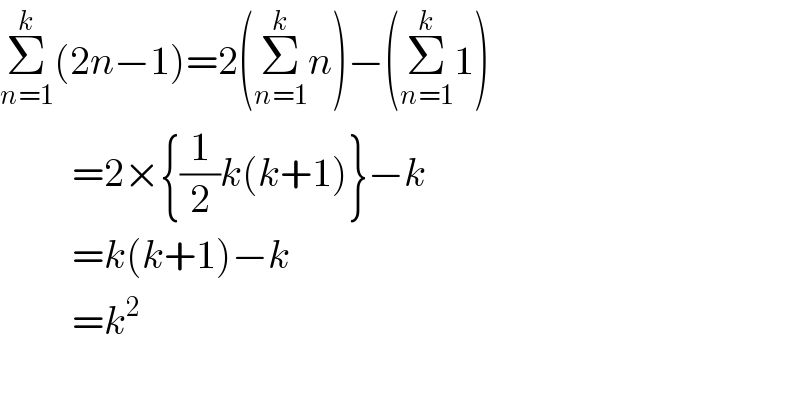
Σ_(n=1) ^k (2n−1)=2(Σ_(n=1) ^k n)−(Σ_(n=1) ^k 1) =2×{(1/2)k(k+1)}−k =k(k+1)−k =k^2

$$\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\left(\mathrm{2}{n}−\mathrm{1}\right)=\mathrm{2}\left(\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}{n}\right)−\left(\underset{{n}=\mathrm{1}} {\overset{{k}} {\sum}}\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{2}×\left\{\frac{\mathrm{1}}{\mathrm{2}}{k}\left({k}+\mathrm{1}\right)\right\}−{k} \\ $$$$\:\:\:\:\:\:\:\:\:={k}\left({k}+\mathrm{1}\right)−{k} \\ $$$$\:\:\:\:\:\:\:\:\:={k}^{\mathrm{2}} \\ $$$$ \\ $$

Facebook Tweet Pin

S-n-t-k-2n-1-S-

Leave a Reply Cancel reply