Question Number 143597 by Videz last updated on 16/Jun/21
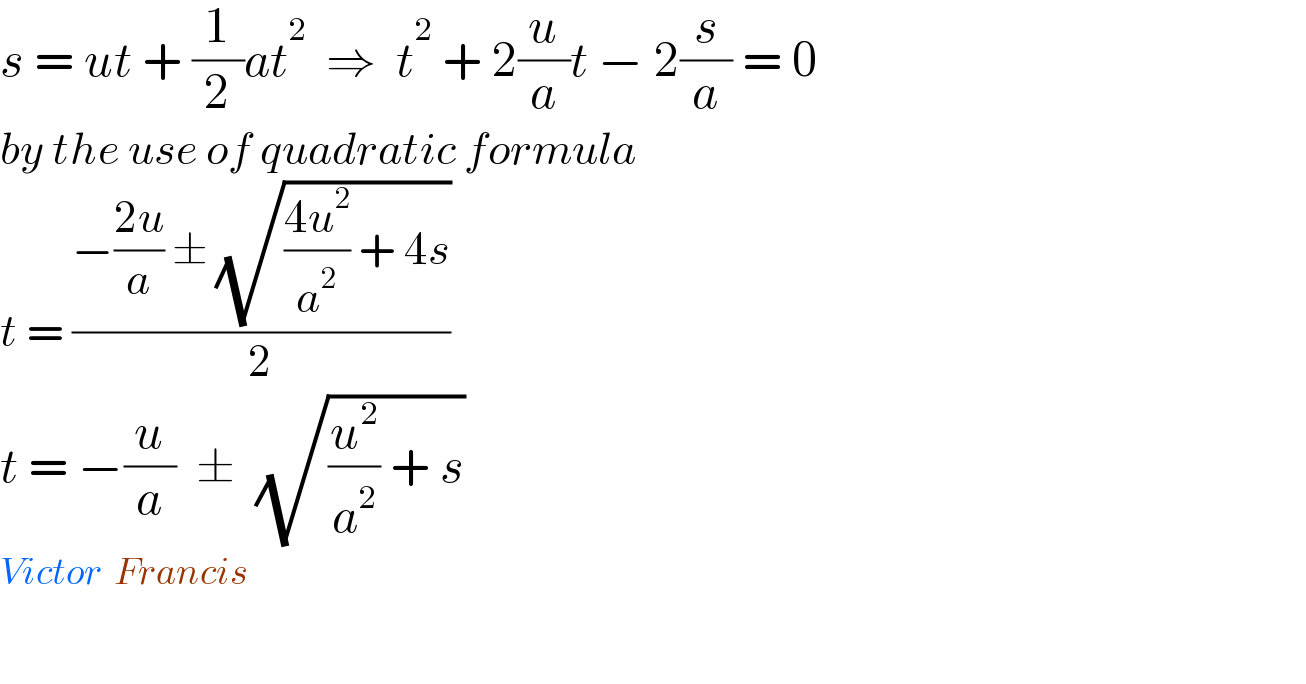
$${s}\:=\:{ut}\:+\:\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \:\:\Rightarrow\:\:{t}^{\mathrm{2}} \:+\:\mathrm{2}\frac{{u}}{{a}}{t}\:−\:\mathrm{2}\frac{{s}}{{a}}\:=\:\mathrm{0} \\ $$$${by}\:{the}\:{use}\:{of}\:{quadratic}\:{formula} \\ $$$${t}\:=\:\frac{−\frac{\mathrm{2}{u}}{{a}}\:\pm\:\sqrt{\frac{\mathrm{4}{u}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\:\mathrm{4}{s}}}{\mathrm{2}} \\ $$$${t}\:=\:−\frac{{u}}{{a}}\:\:\pm\:\:\sqrt{\frac{{u}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:+\:{s}} \\ $$$${Victor}\:\:{Francis} \\ $$$$ \\ $$$$ \\ $$
