Question Number 12768 by Joel577 last updated on 01/May/17
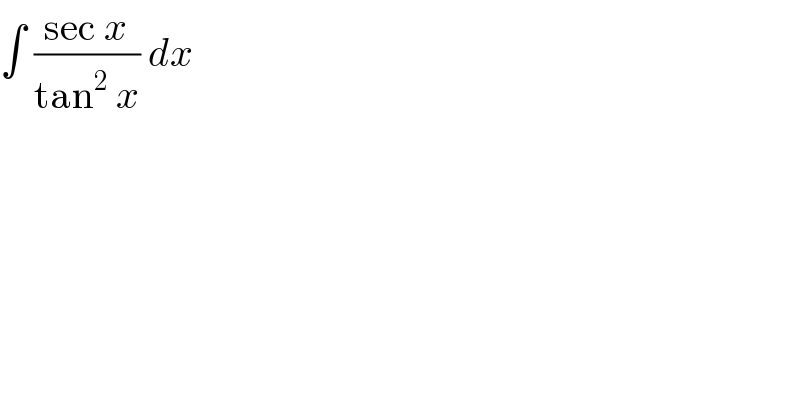
$$\int\:\frac{\mathrm{sec}\:{x}}{\mathrm{tan}^{\mathrm{2}} \:{x}}\:{dx} \\ $$
Answered by prakash jain last updated on 01/May/17
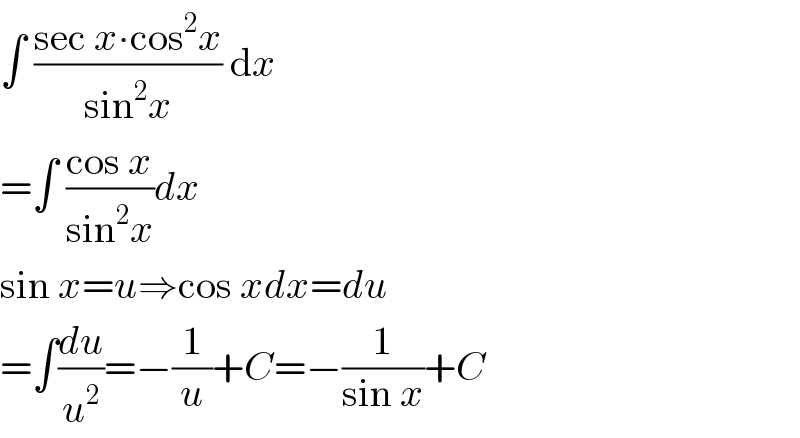
$$\int\:\frac{\mathrm{sec}\:{x}\centerdot\mathrm{cos}^{\mathrm{2}} {x}}{\mathrm{sin}^{\mathrm{2}} {x}}\:\mathrm{d}{x} \\ $$$$=\int\:\frac{\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{2}} {x}}{dx} \\ $$$$\mathrm{sin}\:{x}={u}\Rightarrow\mathrm{cos}\:{xdx}={du} \\ $$$$=\int\frac{{du}}{{u}^{\mathrm{2}} }=−\frac{\mathrm{1}}{{u}}+{C}=−\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+{C} \\ $$
Commented by Joel577 last updated on 01/May/17
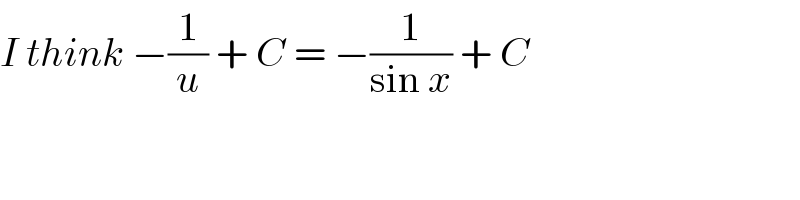
$${I}\:{think}\:−\frac{\mathrm{1}}{{u}}\:+\:{C}\:=\:−\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\:+\:{C} \\ $$
Commented by prakash jain last updated on 01/May/17

$${yes}.\:{corrected}. \\ $$
Commented by Joel577 last updated on 01/May/17
$${thank}\:{you}\:{very}\:{much} \\ $$
