Question Number 141362 by cesarL last updated on 17/May/21
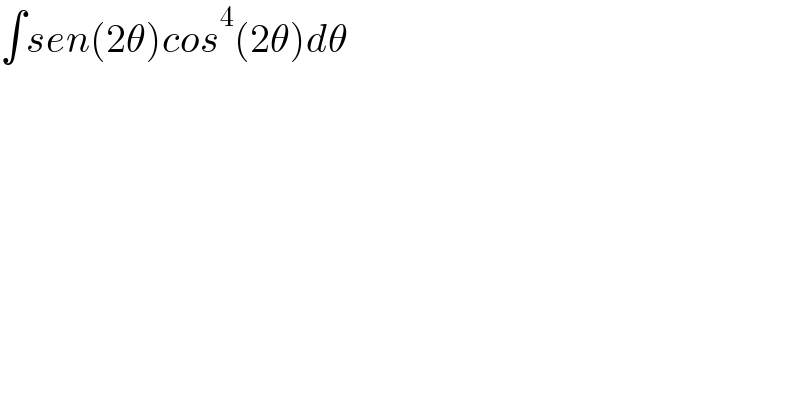
$$\int{sen}\left(\mathrm{2}\theta\right){cos}^{\mathrm{4}} \left(\mathrm{2}\theta\right){d}\theta \\ $$
Answered by bemath last updated on 17/May/21
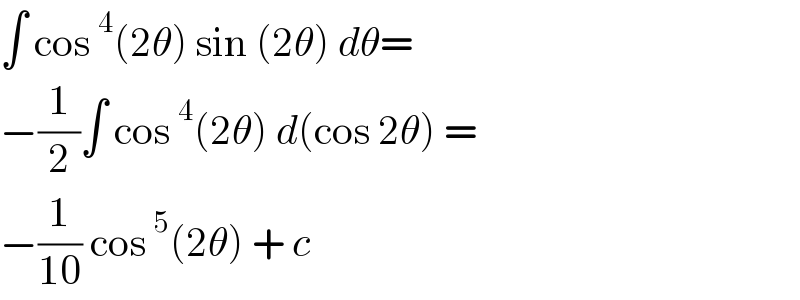
$$\int\:\mathrm{cos}\:^{\mathrm{4}} \left(\mathrm{2}\theta\right)\:\mathrm{sin}\:\left(\mathrm{2}\theta\right)\:{d}\theta= \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{cos}\:^{\mathrm{4}} \left(\mathrm{2}\theta\right)\:{d}\left(\mathrm{cos}\:\mathrm{2}\theta\right)\:= \\ $$$$−\frac{\mathrm{1}}{\mathrm{10}}\:\mathrm{cos}\:^{\mathrm{5}} \left(\mathrm{2}\theta\right)\:+\:{c}\: \\ $$
