Question Number 138756 by 676597498 last updated on 17/Apr/21
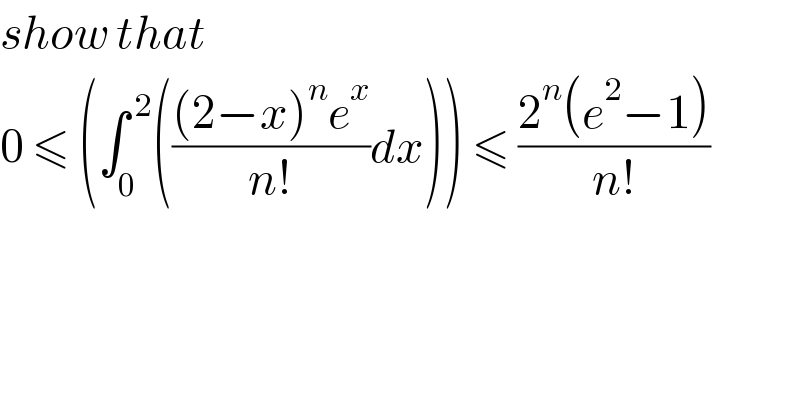
$${show}\:{that} \\ $$$$\mathrm{0}\:\leqslant\:\left(\int_{\mathrm{0}} ^{\:\mathrm{2}} \left(\frac{\left(\mathrm{2}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\right)\right)\:\leqslant\:\frac{\mathrm{2}^{{n}} \left({e}^{\mathrm{2}} −\mathrm{1}\right)}{{n}!} \\ $$
Answered by mr W last updated on 18/Apr/21
![for 0≤x≤2: 0≤2−x≤2 for n≥1: 0≤(2−x)^n ≤2^n 0≤(((2−x)^n e^x )/(n!))≤((2^n e^x )/(n!)) ∫_0 ^2 0dx≤∫_0 ^2 (((2−x)^n e^x )/(n!))dx≤∫_0 ^2 ((2^n e^x )/(n!))dx 0≤∫_0 ^2 (((2−x)^n e^x )/(n!))dx≤((2^n e^x )/(n!))[e^x ]_0 ^2 0≤∫_0 ^2 (((2−x)^n e^x )/(n!))dx≤((2^n (e^2 −1))/(n!))](https://www.tinkutara.com/question/Q138778.png)
$${for}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{2}: \\ $$$$\mathrm{0}\leqslant\mathrm{2}−{x}\leqslant\mathrm{2} \\ $$$${for}\:{n}\geqslant\mathrm{1}: \\ $$$$\mathrm{0}\leqslant\left(\mathrm{2}−{x}\right)^{{n}} \leqslant\mathrm{2}^{{n}} \\ $$$$\mathrm{0}\leqslant\frac{\left(\mathrm{2}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}\leqslant\frac{\mathrm{2}^{{n}} {e}^{{x}} }{{n}!} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{0}{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\left(\mathrm{2}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{2}^{{n}} {e}^{{x}} }{{n}!}{dx} \\ $$$$\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\left(\mathrm{2}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\leqslant\frac{\mathrm{2}^{{n}} {e}^{{x}} }{{n}!}\left[{e}^{{x}} \right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\left(\mathrm{2}−{x}\right)^{{n}} {e}^{{x}} }{{n}!}{dx}\leqslant\frac{\mathrm{2}^{{n}} \left({e}^{\mathrm{2}} −\mathrm{1}\right)}{{n}!} \\ $$
