Question Number 136210 by Ar Brandon last updated on 19/Mar/21
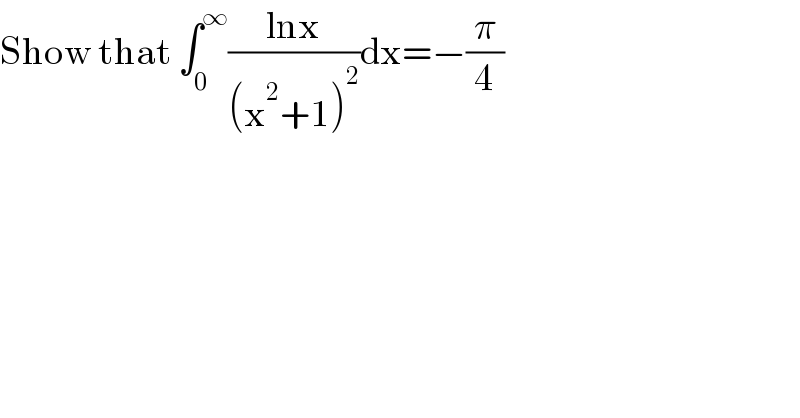
$$\mathrm{Show}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=−\frac{\pi}{\mathrm{4}} \\ $$
Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Oh}\:!\:\mathrm{Thank}\:\mathrm{You}\:\mathrm{Sir} \\ $$😃
Commented by Ar Brandon last updated on 19/Mar/21
![Ω=∫_0 ^∞ ((lnx)/((x^2 +1)^2 ))dx =(∂/∂s)∣_(s=0) ∫_0 ^∞ (x^s /((x^2 +1)^2 ))dx=^(u=x^2 ) (∂/∂s)∣_(s=0) (1/2)∫_0 ^∞ (u^((s/2)−(1/2)) /((u+1)^2 ))du =(∂/∂s)∣_(s=0) (1/2)β((s/2)+(1/2), (3/2)−(s/2))=(∂/∂s)∣_(s=0) (1/2)Γ((s/2)+(1/2))Γ((3/2)−(s/2)) =(1/2)∣_(s=0) Γ((s/2)+(1/2))Γ′((3/2)−(s/2))+Γ((3/2)−(s/2))Γ′((s/2)+(1/2)) =(1/2)∙(1/2)Γ((1/2))Γ((3/2))[ψ((1/2))−ψ((3/2))]=(π/8)[ψ((1/2))−ψ((1/2))−2]=−(π/4)](https://www.tinkutara.com/question/Q136212.png)
$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\:\:\:\:\:=\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{s}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\overset{\mathrm{u}=\mathrm{x}^{\mathrm{2}} } {=}\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{\frac{\mathrm{s}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{u}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{du} \\ $$$$\:\:\:\:\:=\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right)=\frac{\partial}{\partial\mathrm{s}}\mid_{\mathrm{s}=\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mid_{\mathrm{s}=\mathrm{0}} \Gamma\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma'\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right)+\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{s}}{\mathrm{2}}\right)\Gamma'\left(\frac{\mathrm{s}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\left[\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right]=\frac{\pi}{\mathrm{8}}\left[\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\right]=−\frac{\pi}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 19/Mar/21
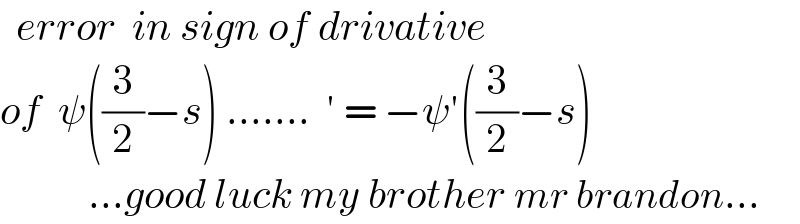
$$\:\:{error}\:\:{in}\:{sign}\:{of}\:{drivative} \\ $$$${of}\:\:\psi\left(\frac{\mathrm{3}}{\mathrm{2}}−{s}\right)\:…….\:\:'\:=\:−\psi'\left(\frac{\mathrm{3}}{\mathrm{2}}−{s}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:…{good}\:{luck}\:{my}\:{brother}\:{mr}\:{brandon}… \\ $$
Answered by mnjuly1970 last updated on 19/Mar/21
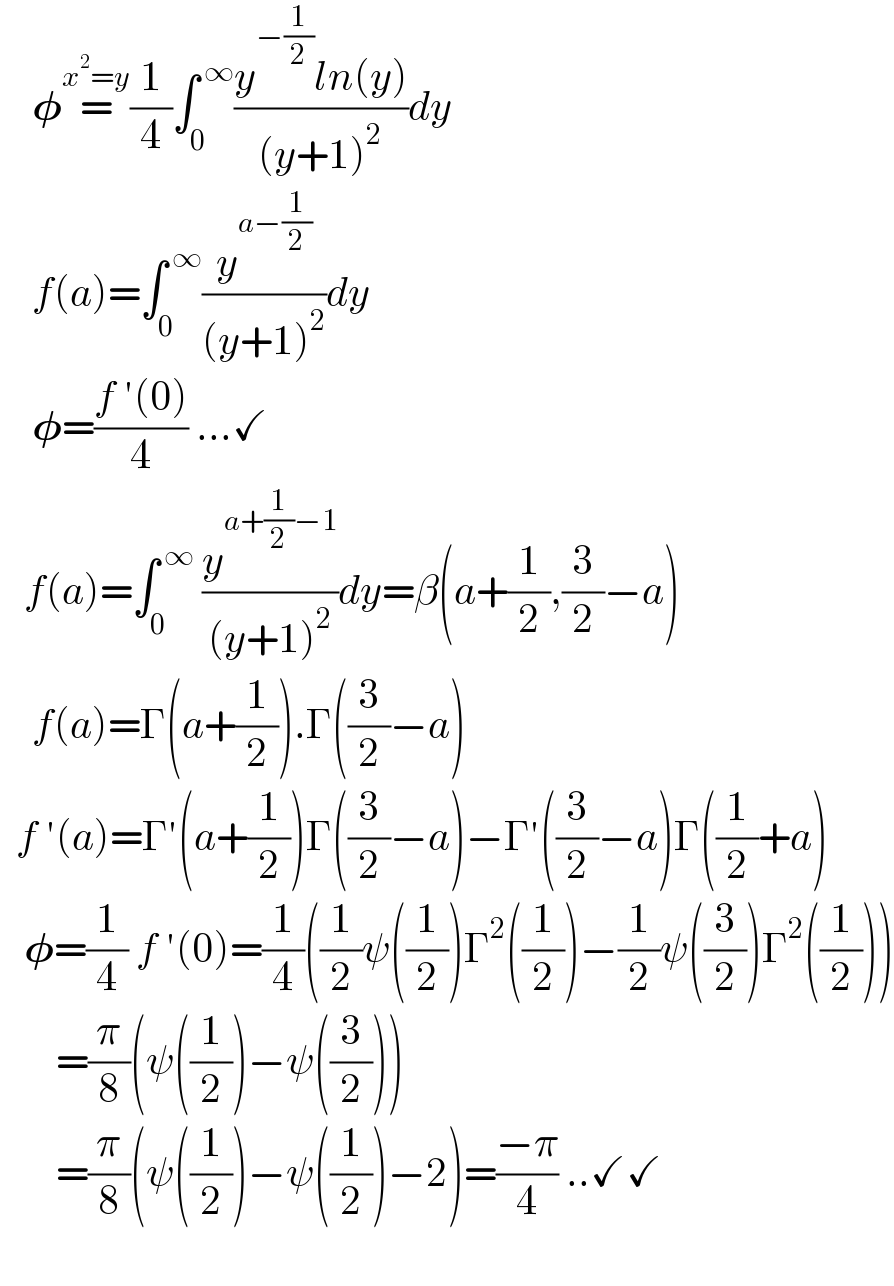
$$\:\:\:\:\boldsymbol{\phi}\overset{{x}^{\mathrm{2}} ={y}} {=}\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\:\infty} \frac{{y}^{−\frac{\mathrm{1}}{\mathrm{2}}} {ln}\left({y}\right)}{\left({y}+\mathrm{1}\right)^{\mathrm{2}} }{dy} \\ $$$$\:\:\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{y}^{{a}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left({y}+\mathrm{1}\right)^{\mathrm{2}} }{dy} \\ $$$$\:\:\:\:\boldsymbol{\phi}=\frac{{f}\:'\left(\mathrm{0}\right)}{\mathrm{4}}\:…\checkmark \\ $$$$\:\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{y}^{{a}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\left({y}+\mathrm{1}\right)^{\mathrm{2}} }{dy}=\beta\left({a}+\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}−{a}\right) \\ $$$$\:\:\:\:{f}\left({a}\right)=\Gamma\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right) \\ $$$$\:\:{f}\:'\left({a}\right)=\Gamma'\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)−\Gamma'\left(\frac{\mathrm{3}}{\mathrm{2}}−{a}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+{a}\right) \\ $$$$\:\:\:\boldsymbol{\phi}=\frac{\mathrm{1}}{\mathrm{4}}\:{f}\:'\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{8}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:\:=\frac{\pi}{\mathrm{8}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\right)=\frac{−\pi}{\mathrm{4}}\:..\checkmark\checkmark \\ $$$$\:\: \\ $$
Answered by Dwaipayan Shikari last updated on 19/Mar/21
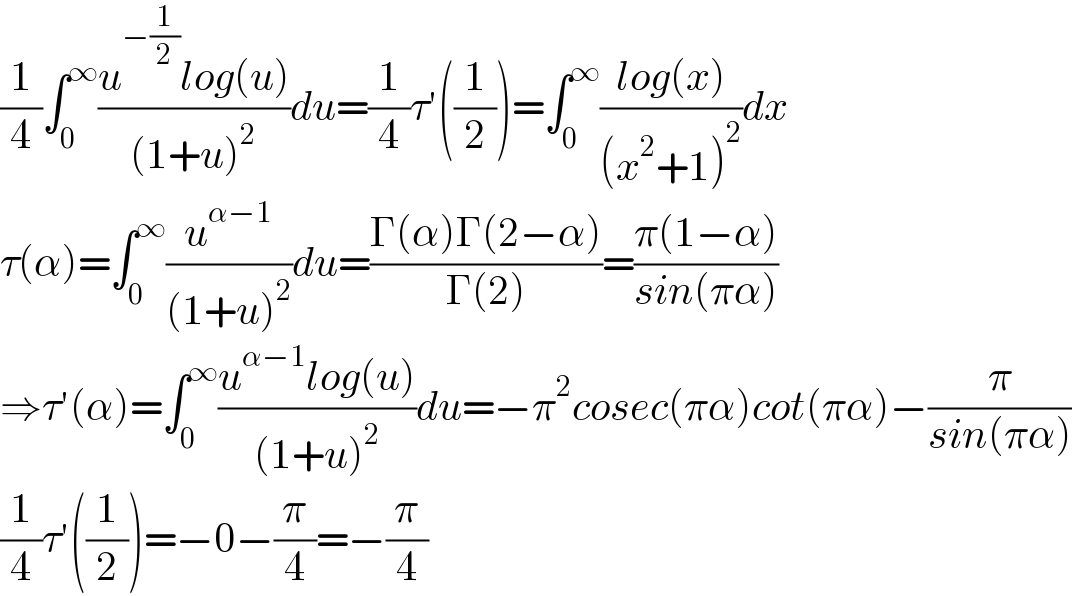
$$\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} {log}\left({u}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}=\frac{\mathrm{1}}{\mathrm{4}}\tau'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\tau\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alpha−\mathrm{1}} }{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}=\frac{\Gamma\left(\alpha\right)\Gamma\left(\mathrm{2}−\alpha\right)}{\Gamma\left(\mathrm{2}\right)}=\frac{\pi\left(\mathrm{1}−\alpha\right)}{{sin}\left(\pi\alpha\right)} \\ $$$$\Rightarrow\tau'\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\alpha−\mathrm{1}} {log}\left({u}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{du}=−\pi^{\mathrm{2}} {cosec}\left(\pi\alpha\right){cot}\left(\pi\alpha\right)−\frac{\pi}{{sin}\left(\pi\alpha\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\tau'\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{0}−\frac{\pi}{\mathrm{4}}=−\frac{\pi}{\mathrm{4}} \\ $$
Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Thanks}\:\mathrm{bro} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Mar/21

$$ \\ $$😃
Answered by Ajetunmobi last updated on 19/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{have}}\:\boldsymbol{\mathrm{drop}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{solution}}\:\boldsymbol{\mathrm{before}}\:\boldsymbol{\mathrm{here}} \\ $$
Commented by Ar Brandon last updated on 19/Mar/21

$$\mathrm{Alright}\:! \\ $$$$\mathrm{Before}\:\mathrm{posting}\:\mathrm{I}\:\mathrm{used}\:\mathrm{the}\:\mathrm{search}\:\mathrm{option}\: \\ $$$$\mathrm{to}\:\mathrm{check}\:\mathrm{if}\:\mathrm{it}\:\mathrm{was}\:\mathrm{previously}\:\mathrm{posted}\:\mathrm{but}\: \\ $$$$\mathrm{couldn}'\mathrm{t}\:\mathrm{find}\:\mathrm{it}.\:\mathrm{Thank}\:\mathrm{You}\:\mathrm{Sir} \\ $$
Commented by Ajetunmobi last updated on 19/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{ok}} \\ $$
Answered by Ajetunmobi last updated on 19/Mar/21

Answered by mathmax by abdo last updated on 19/Mar/21
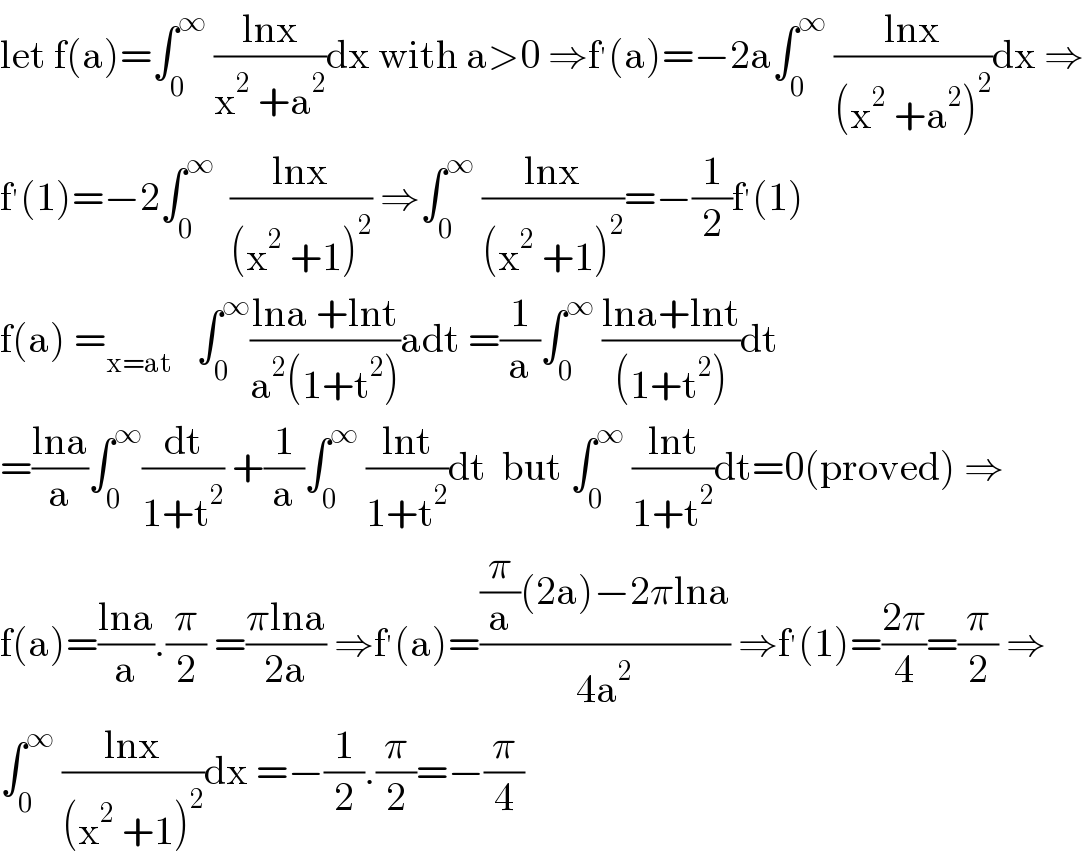
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{with}\:\mathrm{a}>\mathrm{0}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\mathrm{2a}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{1}\right)=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{f}^{'} \left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=_{\mathrm{x}=\mathrm{at}} \:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lna}\:+\mathrm{lnt}}{\mathrm{a}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{adt}\:=\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lna}+\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt} \\ $$$$=\frac{\mathrm{lna}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:\mathrm{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\mathrm{0}\left(\mathrm{proved}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{lna}}{\mathrm{a}}.\frac{\pi}{\mathrm{2}}\:=\frac{\pi\mathrm{lna}}{\mathrm{2a}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=\frac{\frac{\pi}{\mathrm{a}}\left(\mathrm{2a}\right)−\mathrm{2}\pi\mathrm{lna}}{\mathrm{4a}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)=\frac{\mathrm{2}\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{2}}=−\frac{\pi}{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 19/Mar/21
$$\mathrm{folow}\:\mathrm{my}\:\mathrm{facebook}\:\:\left(\mathrm{abdo}\:\mathrm{imad}\right) \\ $$
Commented by Ajetunmobi last updated on 19/Mar/21

$$ \\ $$$$\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{mathmax}}\:\boldsymbol{\mathrm{by}}\:\boldsymbol{\mathrm{abdo}} \\ $$$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{chat}}\:\boldsymbol{\mathrm{privately}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{to}} \\ $$$$\boldsymbol{\mathrm{talk}}\:\boldsymbol{\mathrm{about}}\:\boldsymbol{\mathrm{something}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{\mathrm{you}}\: \\ $$$$\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{send}}\:\boldsymbol{\mathrm{me}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{whatsapp}}\:\boldsymbol{\mathrm{number}} \\ $$$$\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{your}}\:\boldsymbol{\mathrm{facebook}}\:\boldsymbol{\mathrm{name}}\: \\ $$$$\boldsymbol{\mathrm{Thanks}} \\ $$
Commented by Ajetunmobi last updated on 20/Mar/21
$$ \\ $$$$\boldsymbol{\mathrm{there}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{many}}\:\boldsymbol{\mathrm{abdo}}\:\boldsymbol{\mathrm{imad}}\:\boldsymbol{\mathrm{there}}\: \\ $$$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{recognize}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{sir}}? \\ $$
