Menu Close

show-that-1-gamma-function-lim-n-H-n-ln-n-

Tinku Tara 0 Comments
Pin




Question Number 2818 by prakash jain last updated on 27/Nov/15
show that Γ′(1)=−γ Γ gamma function γ=lim_(n→∞) [H_n −ln n]
$$\mathrm{show}\:\mathrm{that} \\ $$$$\Gamma'\left(\mathrm{1}\right)=−\gamma \\ $$$$\Gamma\:\mathrm{gamma}\:\mathrm{function} \\ $$$$\gamma=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left[\mathrm{H}_{{n}} −\mathrm{ln}\:{n}\right] \\ $$
Answered by 123456 last updated on 30/Nov/15
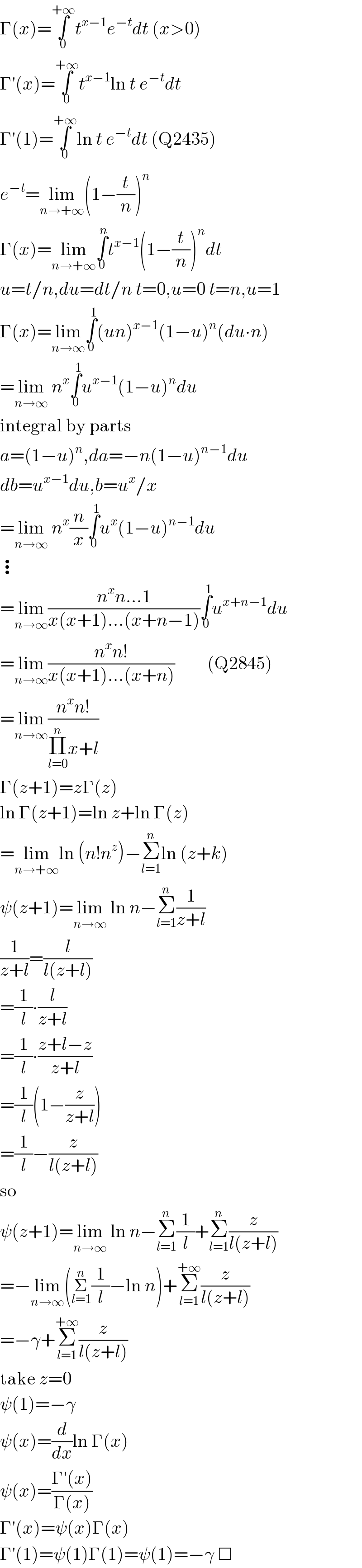
Γ(x)=∫_0 ^(+∞) t^(x−1) e^(−t) dt (x>0) Γ′(x)=∫_0 ^(+∞) t^(x−1) ln t e^(−t) dt Γ′(1)=∫_0 ^(+∞) ln t e^(−t) dt (Q2435) e^(−t) =lim_(n→+∞) (1−(t/n))^n Γ(x)=lim_(n→+∞) ∫_0 ^n t^(x−1) (1−(t/n))^n dt u=t/n,du=dt/n t=0,u=0 t=n,u=1 Γ(x)=lim_(n→∞) ∫_0 ^1 (un)^(x−1) (1−u)^n (du∙n) =lim_(n→∞) n^x ∫_0 ^1 u^(x−1) (1−u)^n du integral by parts a=(1−u)^n ,da=−n(1−u)^(n−1) du db=u^(x−1) du,b=u^x /x =lim_(n→∞) n^x (n/x)∫_0 ^1 u^x (1−u)^(n−1) du ⋮ =lim_(n→∞) ((n^x n...1)/(x(x+1)...(x+n−1)))∫_0 ^1 u^(x+n−1) du =lim_(n→∞) ((n^x n!)/(x(x+1)...(x+n))) (Q2845) =lim_(n→∞) ((n^x n!)/(Π_(l=0) ^n x+l)) Γ(z+1)=zΓ(z) ln Γ(z+1)=ln z+ln Γ(z) =lim_(n→+∞) ln (n!n^z )−Σ_(l=1) ^n ln (z+k) ψ(z+1)=lim_(n→∞) ln n−Σ_(l=1) ^n (1/(z+l)) (1/(z+l))=(l/(l(z+l))) =(1/l)∙(l/(z+l)) =(1/l)∙((z+l−z)/(z+l)) =(1/l)(1−(z/(z+l))) =(1/l)−(z/(l(z+l))) so ψ(z+1)=lim_(n→∞) ln n−Σ_(l=1) ^n (1/l)+Σ_(l=1) ^n (z/(l(z+l))) =−lim_(n→∞) (Σ_(l=1) ^n (1/l)−ln n)+Σ_(l=1) ^(+∞) (z/(l(z+l))) =−γ+Σ_(l=1) ^(+∞) (z/(l(z+l))) take z=0 ψ(1)=−γ ψ(x)=(d/dx)ln Γ(x) ψ(x)=((Γ′(x))/(Γ(x))) Γ′(x)=ψ(x)Γ(x) Γ′(1)=ψ(1)Γ(1)=ψ(1)=−γ □
$$\Gamma\left({x}\right)=\underset{\mathrm{0}} {\overset{+\infty} {\int}}{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\:\left({x}>\mathrm{0}\right) \\ $$$$\Gamma'\left({x}\right)=\underset{\mathrm{0}} {\overset{+\infty} {\int}}{t}^{{x}−\mathrm{1}} \mathrm{ln}\:{t}\:{e}^{−{t}} {dt} \\ $$$$\Gamma'\left(\mathrm{1}\right)=\underset{\mathrm{0}} {\overset{+\infty} {\int}}\mathrm{ln}\:{t}\:{e}^{−{t}} {dt}\:\left(\mathrm{Q2435}\right) \\ $$$${e}^{−{t}} =\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} \\ $$$$\Gamma\left({x}\right)=\underset{{n}\rightarrow+\infty} {\mathrm{lim}}\underset{\mathrm{0}} {\overset{{n}} {\int}}{t}^{{x}−\mathrm{1}} \left(\mathrm{1}−\frac{{t}}{{n}}\right)^{{n}} {dt} \\ $$$${u}={t}/{n},{du}={dt}/{n}\:{t}=\mathrm{0},{u}=\mathrm{0}\:{t}={n},{u}=\mathrm{1} \\ $$$$\Gamma\left({x}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({un}\right)^{{x}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} \left({du}\centerdot{n}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{{x}} \underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{u}^{{x}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{{n}} {du} \\ $$$$\mathrm{integral}\:\mathrm{by}\:\mathrm{parts} \\ $$$${a}=\left(\mathrm{1}−{u}\right)^{{n}} ,{da}=−{n}\left(\mathrm{1}−{u}\right)^{{n}−\mathrm{1}} {du} \\ $$$${db}={u}^{{x}−\mathrm{1}} {du},{b}={u}^{{x}} /{x} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{n}^{{x}} \frac{{n}}{{x}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{u}^{{x}} \left(\mathrm{1}−{u}\right)^{{n}−\mathrm{1}} {du} \\ $$$$\vdots \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{x}} {n}…\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)…\left({x}+{n}−\mathrm{1}\right)}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{u}^{{x}+{n}−\mathrm{1}} {du} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{x}} {n}!}{{x}\left({x}+\mathrm{1}\right)…\left({x}+{n}\right)}\:\:\:\:\:\:\:\:\:\left(\mathrm{Q2845}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}^{{x}} {n}!}{\underset{{l}=\mathrm{0}} {\overset{{n}} {\prod}}{x}+{l}} \\ $$$$\Gamma\left({z}+\mathrm{1}\right)={z}\Gamma\left({z}\right) \\ $$$$\mathrm{ln}\:\Gamma\left({z}+\mathrm{1}\right)=\mathrm{ln}\:{z}+\mathrm{ln}\:\Gamma\left({z}\right) \\ $$$$=\underset{{n}\rightarrow+\infty} {\mathrm{lim}ln}\:\left({n}!{n}^{{z}} \right)−\underset{{l}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\:\left({z}+{k}\right) \\ $$$$\psi\left({z}+\mathrm{1}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{ln}\:{n}−\underset{{l}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{z}+{l}} \\ $$$$\frac{\mathrm{1}}{{z}+{l}}=\frac{{l}}{{l}\left({z}+{l}\right)} \\ $$$$=\frac{\mathrm{1}}{{l}}\centerdot\frac{{l}}{{z}+{l}} \\ $$$$=\frac{\mathrm{1}}{{l}}\centerdot\frac{{z}+{l}−{z}}{{z}+{l}} \\ $$$$=\frac{\mathrm{1}}{{l}}\left(\mathrm{1}−\frac{{z}}{{z}+{l}}\right) \\ $$$$=\frac{\mathrm{1}}{{l}}−\frac{{z}}{{l}\left({z}+{l}\right)} \\ $$$$\mathrm{so} \\ $$$$\psi\left({z}+\mathrm{1}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{ln}\:{n}−\underset{{l}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{l}}+\underset{{l}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{z}}{{l}\left({z}+{l}\right)} \\ $$$$=−\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{{l}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{l}}−\mathrm{ln}\:{n}\right)+\underset{{l}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{z}}{{l}\left({z}+{l}\right)} \\ $$$$=−\gamma+\underset{{l}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{{z}}{{l}\left({z}+{l}\right)} \\ $$$$\mathrm{take}\:{z}=\mathrm{0} \\ $$$$\psi\left(\mathrm{1}\right)=−\gamma \\ $$$$\psi\left({x}\right)=\frac{{d}}{{dx}}\mathrm{ln}\:\Gamma\left({x}\right) \\ $$$$\psi\left({x}\right)=\frac{\Gamma'\left({x}\right)}{\Gamma\left({x}\right)} \\ $$$$\Gamma'\left({x}\right)=\psi\left({x}\right)\Gamma\left({x}\right) \\ $$$$\Gamma'\left(\mathrm{1}\right)=\psi\left(\mathrm{1}\right)\Gamma\left(\mathrm{1}\right)=\psi\left(\mathrm{1}\right)=−\gamma\:\Box \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *