Question Number 78311 by mathocean1 last updated on 15/Jan/20
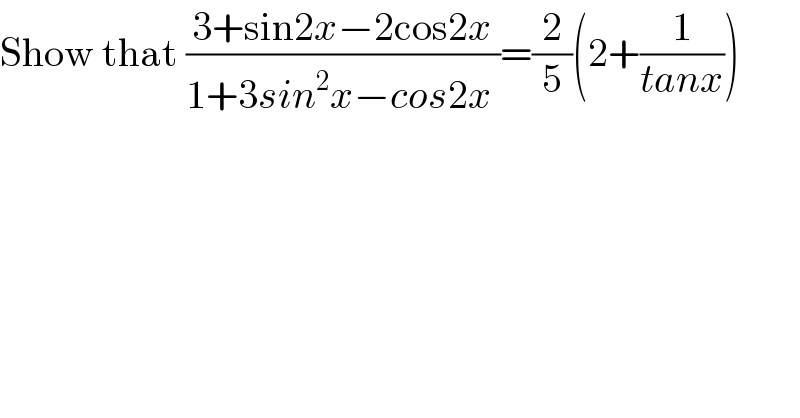
$$\mathrm{Show}\:\mathrm{that}\:\frac{\mathrm{3}+\mathrm{sin2}{x}−\mathrm{2cos2}{x}}{\mathrm{1}+\mathrm{3}{sin}^{\mathrm{2}} {x}−{cos}\mathrm{2}{x}\:}=\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{2}+\frac{\mathrm{1}}{{tanx}}\right) \\ $$
Commented by jagoll last updated on 16/Jan/20
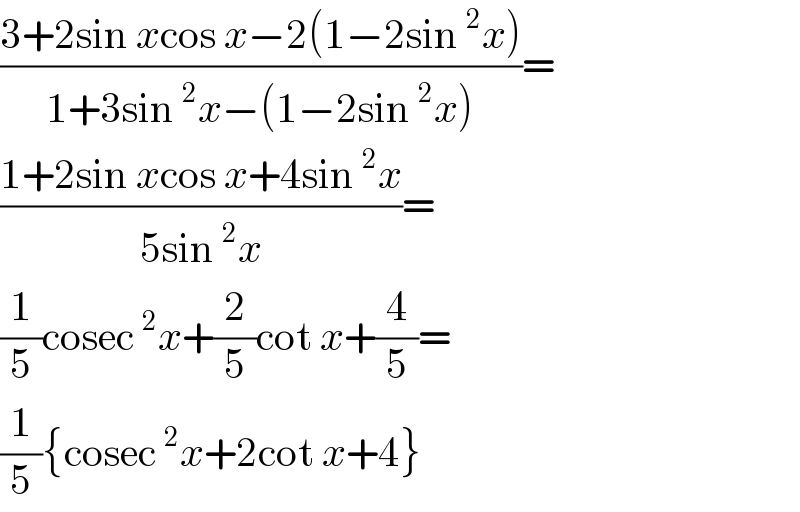
$$\frac{\mathrm{3}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}−\mathrm{2}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)}{\mathrm{1}+\mathrm{3sin}\:^{\mathrm{2}} {x}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\right)}= \\ $$$$\frac{\mathrm{1}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}+\mathrm{4sin}\:^{\mathrm{2}} {x}}{\mathrm{5sin}\:^{\mathrm{2}} {x}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\mathrm{cosec}\:^{\mathrm{2}} {x}+\frac{\mathrm{2}}{\mathrm{5}}\mathrm{cot}\:{x}+\frac{\mathrm{4}}{\mathrm{5}}= \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\left\{\mathrm{cosec}\:^{\mathrm{2}} {x}+\mathrm{2cot}\:{x}+\mathrm{4}\right\} \\ $$
Commented by john santu last updated on 16/Jan/20
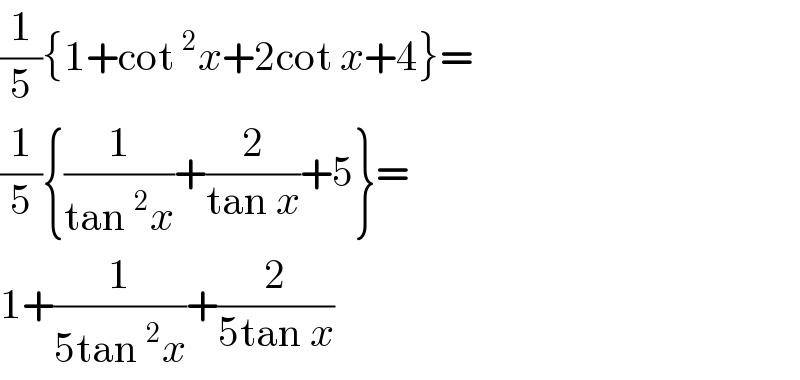
$$\frac{\mathrm{1}}{\mathrm{5}}\left\{\mathrm{1}+\mathrm{cot}\:^{\mathrm{2}} {x}+\mathrm{2cot}\:{x}+\mathrm{4}\right\}= \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\left\{\frac{\mathrm{1}}{\mathrm{tan}\:^{\mathrm{2}} {x}}+\frac{\mathrm{2}}{\mathrm{tan}\:{x}}+\mathrm{5}\right\}= \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{5tan}\:^{\mathrm{2}} {x}}+\frac{\mathrm{2}}{\mathrm{5tan}\:{x}} \\ $$
Answered by mind is power last updated on 15/Jan/20
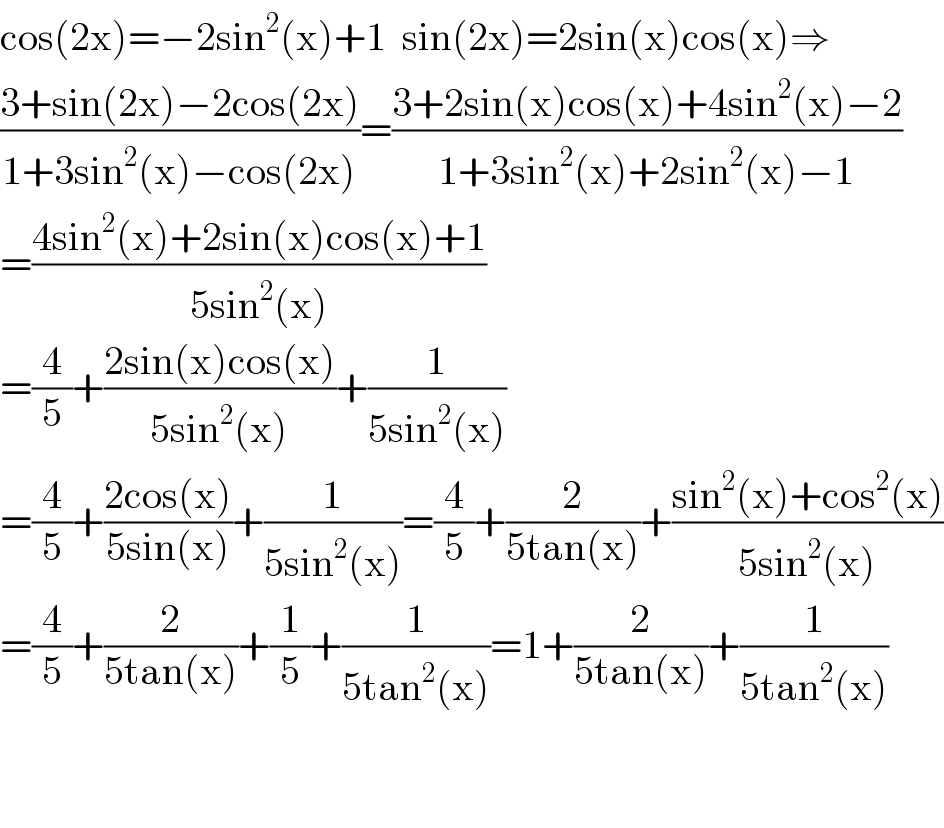
$$\mathrm{cos}\left(\mathrm{2x}\right)=−\mathrm{2sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{1}\:\:\mathrm{sin}\left(\mathrm{2x}\right)=\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)\Rightarrow \\ $$$$\frac{\mathrm{3}+\mathrm{sin}\left(\mathrm{2x}\right)−\mathrm{2cos}\left(\mathrm{2x}\right)}{\mathrm{1}+\mathrm{3sin}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{cos}\left(\mathrm{2x}\right)}=\frac{\mathrm{3}+\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{4sin}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{2}}{\mathrm{1}+\mathrm{3sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2sin}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{1}} \\ $$$$=\frac{\mathrm{4sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{1}}{\mathrm{5sin}^{\mathrm{2}} \left(\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{5sin}^{\mathrm{2}} \left(\mathrm{x}\right)}+\frac{\mathrm{1}}{\mathrm{5sin}^{\mathrm{2}} \left(\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{2cos}\left(\mathrm{x}\right)}{\mathrm{5sin}\left(\mathrm{x}\right)}+\frac{\mathrm{1}}{\mathrm{5sin}^{\mathrm{2}} \left(\mathrm{x}\right)}=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5tan}\left(\mathrm{x}\right)}+\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{5sin}^{\mathrm{2}} \left(\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{5tan}\left(\mathrm{x}\right)}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5tan}^{\mathrm{2}} \left(\mathrm{x}\right)}=\mathrm{1}+\frac{\mathrm{2}}{\mathrm{5tan}\left(\mathrm{x}\right)}+\frac{\mathrm{1}}{\mathrm{5tan}^{\mathrm{2}} \left(\mathrm{x}\right)} \\ $$$$ \\ $$$$ \\ $$
