Question Number 582 by ssahoo last updated on 31/Jan/15
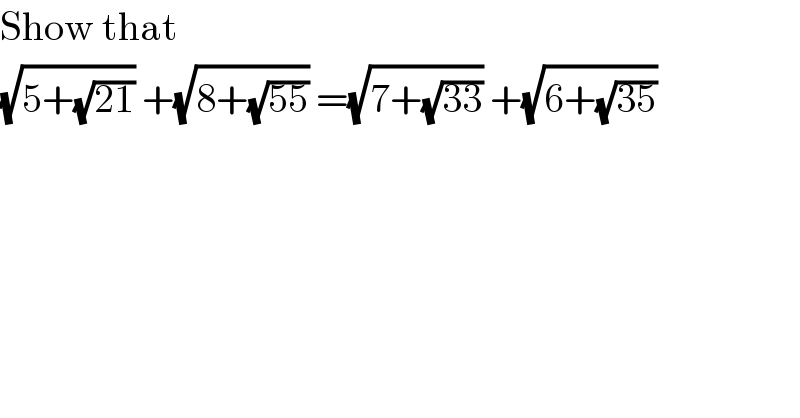
$$\mathrm{Show}\:\mathrm{that} \\ $$$$\sqrt{\mathrm{5}+\sqrt{\mathrm{21}}}\:+\sqrt{\mathrm{8}+\sqrt{\mathrm{55}}}\:=\sqrt{\mathrm{7}+\sqrt{\mathrm{33}}}\:+\sqrt{\mathrm{6}+\sqrt{\mathrm{35}}} \\ $$
Commented by prakash jain last updated on 31/Jan/15
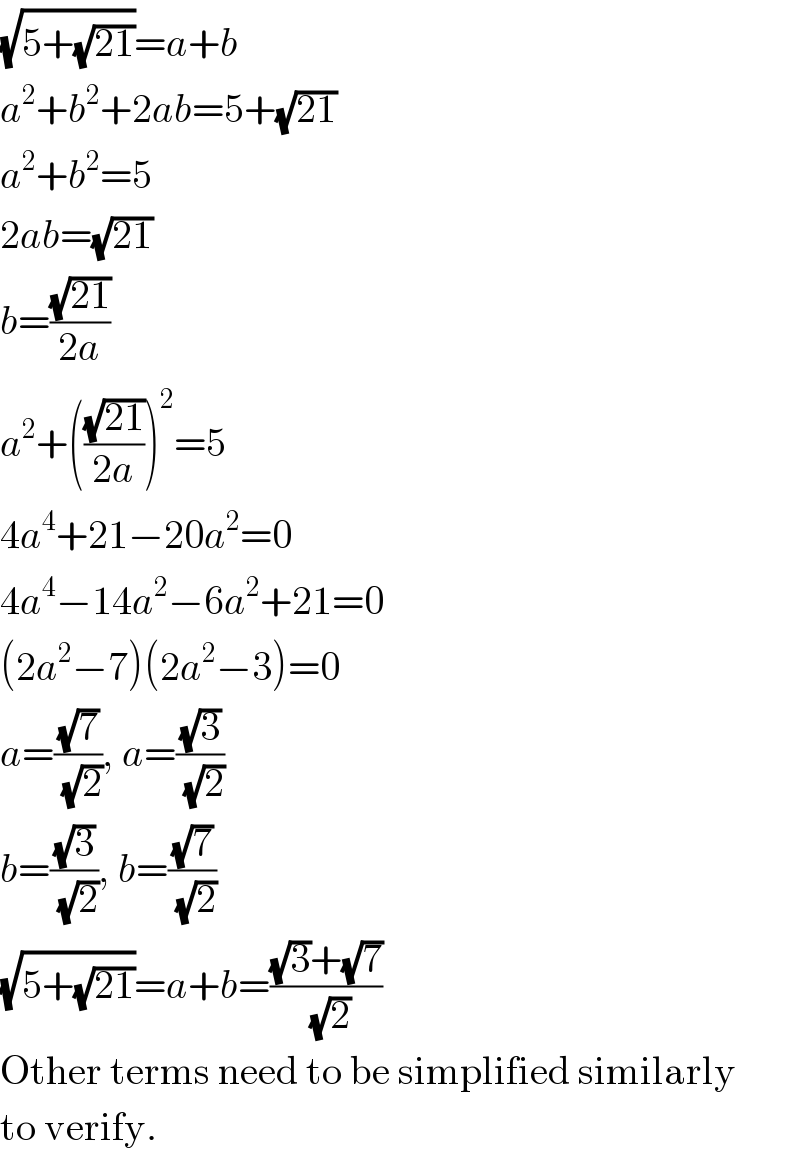
$$\sqrt{\mathrm{5}+\sqrt{\mathrm{21}}}={a}+{b} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}=\mathrm{5}+\sqrt{\mathrm{21}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{5} \\ $$$$\mathrm{2}{ab}=\sqrt{\mathrm{21}} \\ $$$${b}=\frac{\sqrt{\mathrm{21}}}{\mathrm{2}{a}} \\ $$$${a}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{21}}}{\mathrm{2}{a}}\right)^{\mathrm{2}} =\mathrm{5} \\ $$$$\mathrm{4}{a}^{\mathrm{4}} +\mathrm{21}−\mathrm{20}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{a}^{\mathrm{4}} −\mathrm{14}{a}^{\mathrm{2}} −\mathrm{6}{a}^{\mathrm{2}} +\mathrm{21}=\mathrm{0} \\ $$$$\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{7}\right)\left(\mathrm{2}{a}^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$${a}=\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}},\:{a}=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}} \\ $$$${b}=\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}},\:{b}=\frac{\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\sqrt{\mathrm{5}+\sqrt{\mathrm{21}}}={a}+{b}=\frac{\sqrt{\mathrm{3}}+\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{Other}\:\mathrm{terms}\:\mathrm{need}\:\mathrm{to}\:\mathrm{be}\:\mathrm{simplified}\:\mathrm{similarly} \\ $$$$\mathrm{to}\:\mathrm{verify}. \\ $$
Answered by havandip last updated on 16/Aug/15
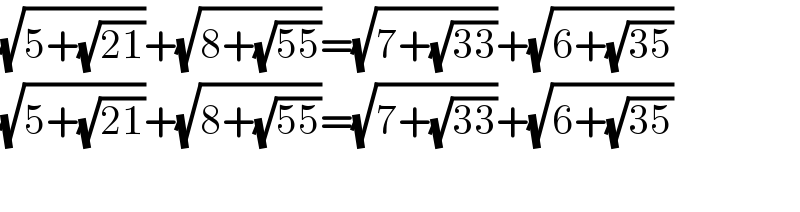
$$\sqrt{\mathrm{5}+\sqrt{\mathrm{21}}}+\sqrt{\mathrm{8}+\sqrt{\mathrm{55}}}=\sqrt{\mathrm{7}+\sqrt{\mathrm{33}}}+\sqrt{\mathrm{6}+\sqrt{\mathrm{35}}} \\ $$$$\sqrt{\mathrm{5}+\sqrt{\mathrm{21}}}+\sqrt{\mathrm{8}+\sqrt{\mathrm{55}}}=\sqrt{\mathrm{7}+\sqrt{\mathrm{33}}}+\sqrt{\mathrm{6}+\sqrt{\mathrm{35}}} \\ $$$$ \\ $$
