Question Number 71852 by Rio Michael last updated on 21/Oct/19
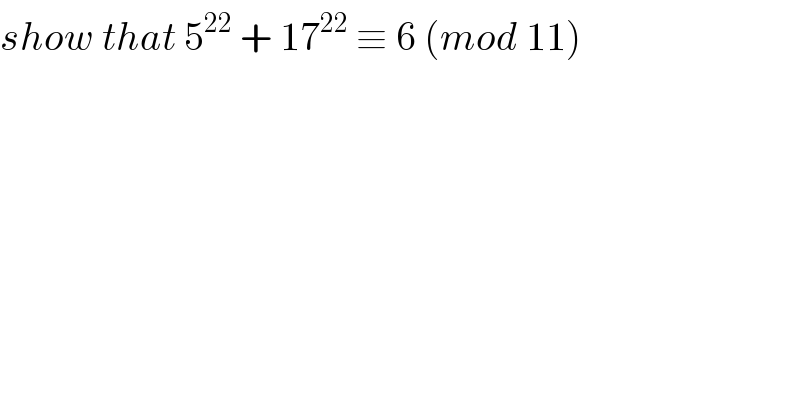
$${show}\:{that}\:\mathrm{5}^{\mathrm{22}} \:+\:\mathrm{17}^{\mathrm{22}} \:\equiv\:\mathrm{6}\:\left({mod}\:\mathrm{11}\right) \\ $$
Answered by mind is power last updated on 21/Oct/19
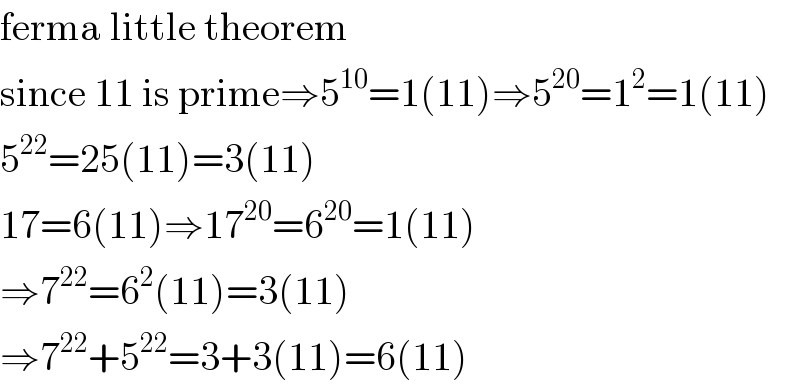
$$\mathrm{ferma}\:\mathrm{little}\:\mathrm{theorem} \\ $$$$\mathrm{since}\:\mathrm{11}\:\mathrm{is}\:\mathrm{prime}\Rightarrow\mathrm{5}^{\mathrm{10}} =\mathrm{1}\left(\mathrm{11}\right)\Rightarrow\mathrm{5}^{\mathrm{20}} =\mathrm{1}^{\mathrm{2}} =\mathrm{1}\left(\mathrm{11}\right) \\ $$$$\mathrm{5}^{\mathrm{22}} =\mathrm{25}\left(\mathrm{11}\right)=\mathrm{3}\left(\mathrm{11}\right) \\ $$$$\mathrm{17}=\mathrm{6}\left(\mathrm{11}\right)\Rightarrow\mathrm{17}^{\mathrm{20}} =\mathrm{6}^{\mathrm{20}} =\mathrm{1}\left(\mathrm{11}\right) \\ $$$$\Rightarrow\mathrm{7}^{\mathrm{22}} =\mathrm{6}^{\mathrm{2}} \left(\mathrm{11}\right)=\mathrm{3}\left(\mathrm{11}\right) \\ $$$$\Rightarrow\mathrm{7}^{\mathrm{22}} +\mathrm{5}^{\mathrm{22}} =\mathrm{3}+\mathrm{3}\left(\mathrm{11}\right)=\mathrm{6}\left(\mathrm{11}\right) \\ $$
Commented by Rio Michael last updated on 21/Oct/19

$${thanks} \\ $$
