Menu Close

Show-that-7-1-7-lt-8-1-8-Also-show-that-100001-100000-lt-1-2-100000-

Tinku Tara 0 Comments
Pin




Question Number 1700 by 112358 last updated on 01/Sep/15
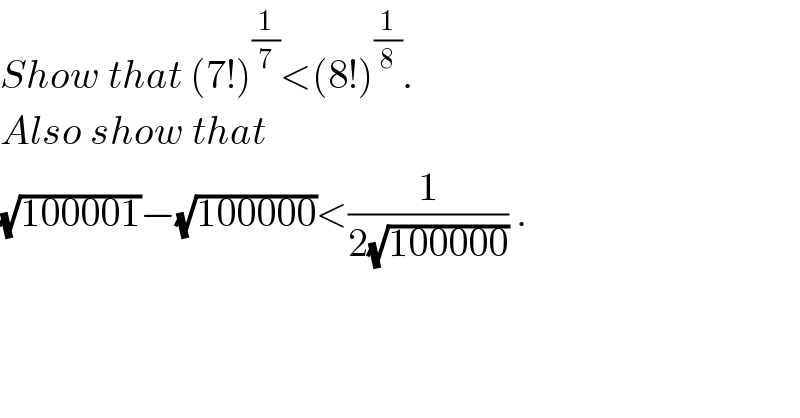
Show that (7!)^(1/7) <(8!)^(1/8) . Also show that (√(100001))−(√(100000))<(1/(2(√(100000)))) .
$${Show}\:{that}\:\left(\mathrm{7}!\right)^{\frac{\mathrm{1}}{\mathrm{7}}} <\left(\mathrm{8}!\right)^{\frac{\mathrm{1}}{\mathrm{8}}} . \\ $$$${Also}\:{show}\:{that}\: \\ $$$$\sqrt{\mathrm{100001}}−\sqrt{\mathrm{100000}}<\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{100000}}}\:. \\ $$$$ \\ $$
Commented by 123456 last updated on 02/Sep/15
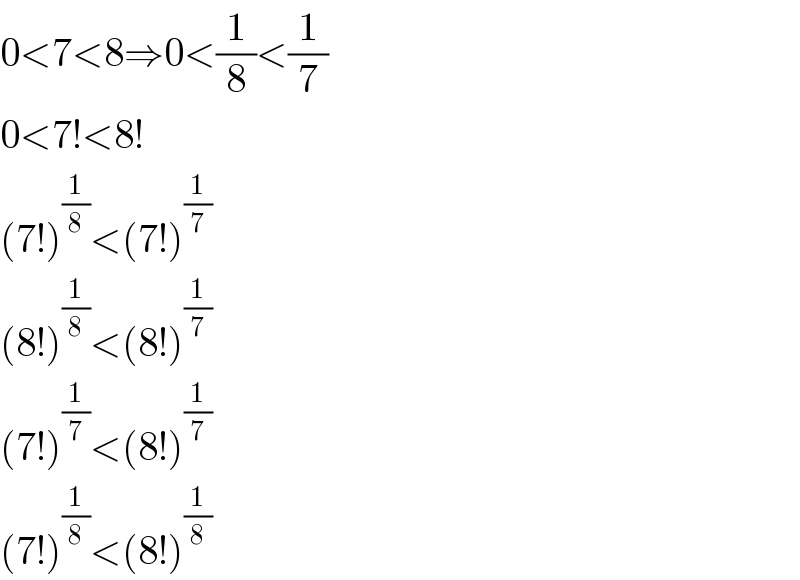
0<7<8⇒0<(1/8)<(1/7) 0<7!<8! (7!)^(1/8) <(7!)^(1/7) (8!)^(1/8) <(8!)^(1/7) (7!)^(1/7) <(8!)^(1/7) (7!)^(1/8) <(8!)^(1/8)
$$\mathrm{0}<\mathrm{7}<\mathrm{8}\Rightarrow\mathrm{0}<\frac{\mathrm{1}}{\mathrm{8}}<\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\mathrm{0}<\mathrm{7}!<\mathrm{8}! \\ $$$$\left(\mathrm{7}!\right)^{\frac{\mathrm{1}}{\mathrm{8}}} <\left(\mathrm{7}!\right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$$\left(\mathrm{8}!\right)^{\frac{\mathrm{1}}{\mathrm{8}}} <\left(\mathrm{8}!\right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$$\left(\mathrm{7}!\right)^{\frac{\mathrm{1}}{\mathrm{7}}} <\left(\mathrm{8}!\right)^{\frac{\mathrm{1}}{\mathrm{7}}} \\ $$$$\left(\mathrm{7}!\right)^{\frac{\mathrm{1}}{\mathrm{8}}} <\left(\mathrm{8}!\right)^{\frac{\mathrm{1}}{\mathrm{8}}} \\ $$
Commented by 123456 last updated on 02/Sep/15
f(x)=(x!)^(1/x)
$${f}\left({x}\right)=\left({x}!\right)^{\frac{\mathrm{1}}{{x}}} \\ $$
Answered by 123456 last updated on 01/Sep/15
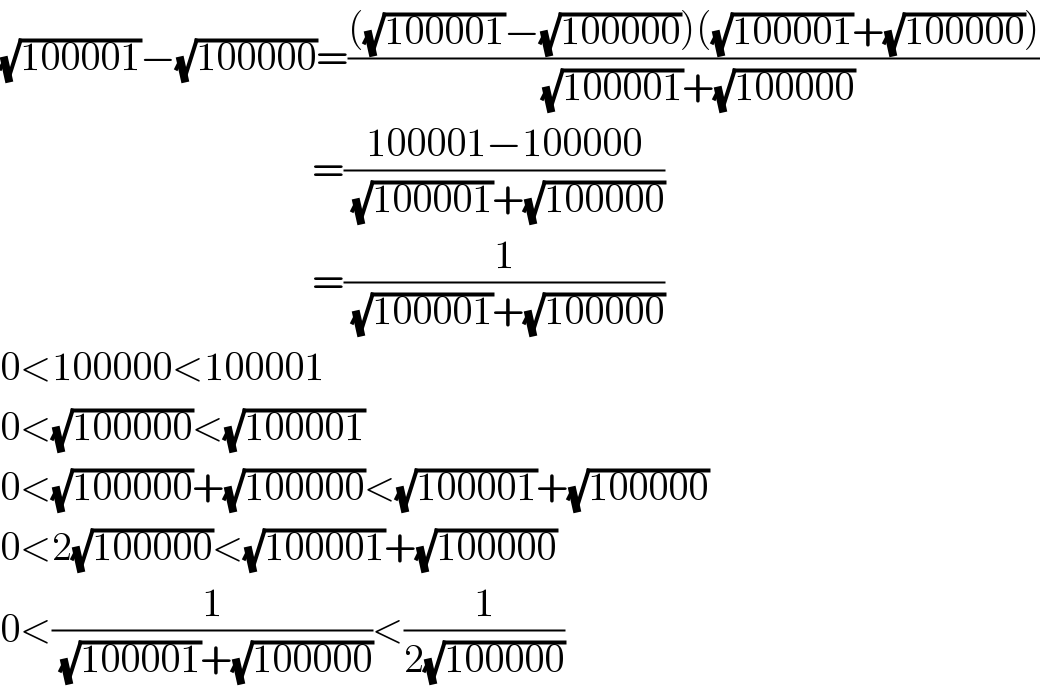
(√(100001))−(√(100000))=((((√(100001))−(√(100000)))((√(100001))+(√(100000))))/( (√(100001))+(√(100000)))) =((100001−100000)/( (√(100001))+(√(100000)))) =(1/( (√(100001))+(√(100000)))) 0<100000<100001 0<(√(100000))<(√(100001)) 0<(√(100000))+(√(100000))<(√(100001))+(√(100000)) 0<2(√(100000))<(√(100001))+(√(100000)) 0<(1/( (√(100001))+(√(100000))))<(1/(2(√(100000))))
$$\sqrt{\mathrm{100001}}−\sqrt{\mathrm{100000}}=\frac{\left(\sqrt{\mathrm{100001}}−\sqrt{\mathrm{100000}}\right)\left(\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}}\right)}{\:\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{100001}−\mathrm{100000}}{\:\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}}} \\ $$$$\mathrm{0}<\mathrm{100000}<\mathrm{100001} \\ $$$$\mathrm{0}<\sqrt{\mathrm{100000}}<\sqrt{\mathrm{100001}} \\ $$$$\mathrm{0}<\sqrt{\mathrm{100000}}+\sqrt{\mathrm{100000}}<\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}} \\ $$$$\mathrm{0}<\mathrm{2}\sqrt{\mathrm{100000}}<\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}} \\ $$$$\mathrm{0}<\frac{\mathrm{1}}{\:\sqrt{\mathrm{100001}}+\sqrt{\mathrm{100000}}}<\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{100000}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *