Question Number 752 by 112358 last updated on 06/Mar/15
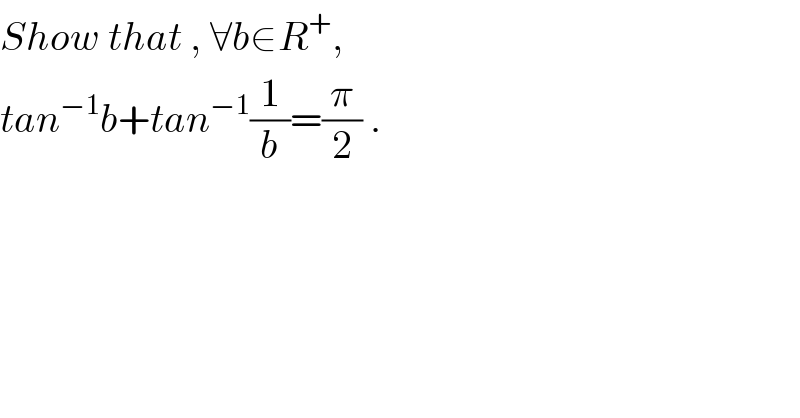
$${Show}\:{that}\:,\:\forall{b}\in{R}^{+} ,\: \\ $$$${tan}^{−\mathrm{1}} {b}+{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{b}}=\frac{\pi}{\mathrm{2}}\:. \\ $$
Answered by 123456 last updated on 06/Mar/15
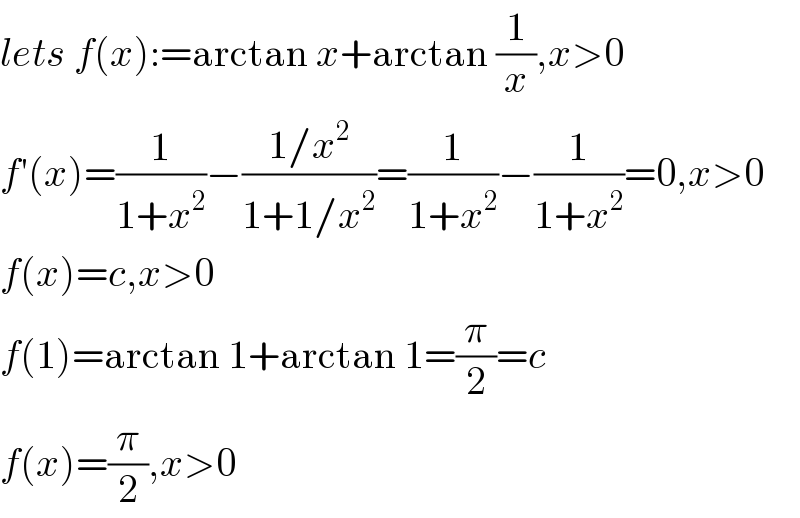
$${lets}\:{f}\left({x}\right):=\mathrm{arctan}\:{x}+\mathrm{arctan}\:\frac{\mathrm{1}}{{x}},{x}>\mathrm{0} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{\mathrm{1}/{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{1}/{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\mathrm{0},{x}>\mathrm{0} \\ $$$${f}\left({x}\right)={c},{x}>\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{arctan}\:\mathrm{1}+\mathrm{arctan}\:\mathrm{1}=\frac{\pi}{\mathrm{2}}={c} \\ $$$${f}\left({x}\right)=\frac{\pi}{\mathrm{2}},{x}>\mathrm{0} \\ $$
