Menu Close

Show-that-f-x-x-2-x-odd-

Tinku Tara 0 Comments
Pin




Question Number 5234 by sanusihammed last updated on 02/May/16
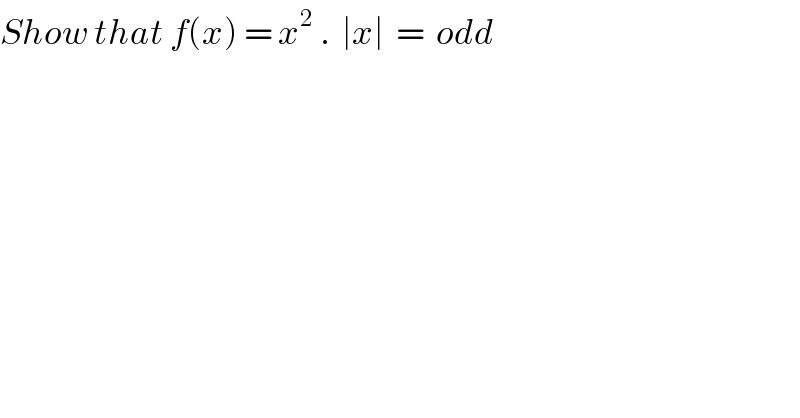
Show that f(x) = x^2 . ∣x∣ = odd
Showthatf(x)=x2.∣x∣=odd
Answered by prakash jain last updated on 02/May/16
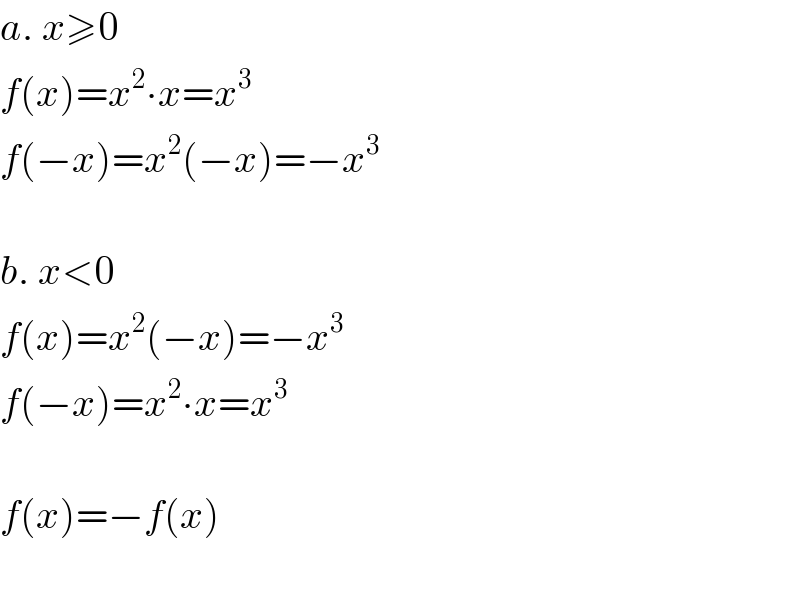
a. x≥0 f(x)=x^2 ∙x=x^3 f(−x)=x^2 (−x)=−x^3 b. x<0 f(x)=x^2 (−x)=−x^3 f(−x)=x^2 ∙x=x^3 f(x)=−f(x)
a.x⩾0f(x)=x2⋅x=x3f(−x)=x2(−x)=−x3b.x<0f(x)=x2(−x)=−x3f(−x)=x2⋅x=x3f(x)=−f(x)

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *