Question Number 1830 by 112358 last updated on 10/Oct/15
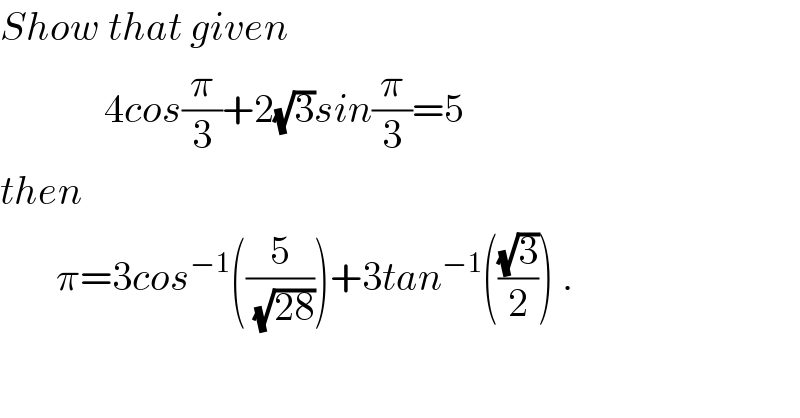
$${Show}\:{that}\:{given} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{cos}\frac{\pi}{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}{sin}\frac{\pi}{\mathrm{3}}=\mathrm{5} \\ $$$${then} \\ $$$$\:\:\:\:\:\:\:\pi=\mathrm{3}{cos}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{28}}}\right)+\mathrm{3}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:. \\ $$
Answered by Rasheed Soomro last updated on 10/Oct/15

$$''\mathrm{4}{cos}\frac{\pi}{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}{sin}\frac{\pi}{\mathrm{3}}\:''\:{is}\:{a}\:{constant}\:{equal}\:{to}\:\mathrm{5} \\ $$$${so}\:{to}\:{say}\:''{if}\:\mathrm{4}{cos}\frac{\pi}{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}{sin}\frac{\pi}{\mathrm{3}}=\mathrm{5}'' \\ $$$${is}\:{meaningless}! \\ $$$${Similarly}\:''\mathrm{3}{cos}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{28}}}\right)+\mathrm{3}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:''\:{is} \\ $$$${also}\:{a}\:{constant}\:{and}\:{it}\:{is}\:{not}\:{dependant}\:{on} \\ $$$$''\mathrm{4}{cos}\frac{\pi}{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}{sin}\frac{\pi}{\mathrm{3}}=\mathrm{5}'' \\ $$$${I}\:{think}\:{that}\:{the}\:\:{Question}\:{is}\:{not}\:{meaningful}! \\ $$
Commented by 112358 last updated on 10/Oct/15

$${The}\:{original}\:{question}\:{is}\:{this}. \\ $$$${Write}\:{down}\:{a}\:{value}\:{of}\:\theta\:{in}\:{the} \\ $$$${interval}\:\:\frac{\pi}{\mathrm{4}}<\theta<\frac{\pi}{\mathrm{2}}\:{that}\:{satisfies} \\ $$$${the}\:{equation} \\ $$$$\mathrm{4}{cos}\theta+\mathrm{2}\sqrt{\mathrm{3}}{sin}\theta=\mathrm{5}.\: \\ $$$${Hence},\:{or}\:{otherwise},\:{show}\:{that} \\ $$$$\pi=\mathrm{3}{cos}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\:\sqrt{\mathrm{28}}}\right)+\mathrm{3}{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right). \\ $$$${Show}\:{that}\: \\ $$$$\pi=\mathrm{4}{sin}^{−\mathrm{1}} \left(\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{10}}\right)−\mathrm{4}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right).\: \\ $$$${I}\:{just}\:{thought}\:{that}\:{from}\:{setting} \\ $$$$\theta=\frac{\pi}{\mathrm{3}}\:{the}\:{question}\:{required}\:\left({though}\right. \\ $$$$\left.{not}\:{strictly}\right)\:{that}\:{you}\:{work}\:{from} \\ $$$$\mathrm{4}{cos}\frac{\pi}{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}{sin}\frac{\pi}{\mathrm{3}}=\mathrm{5}.\: \\ $$
Commented by 112358 last updated on 10/Oct/15
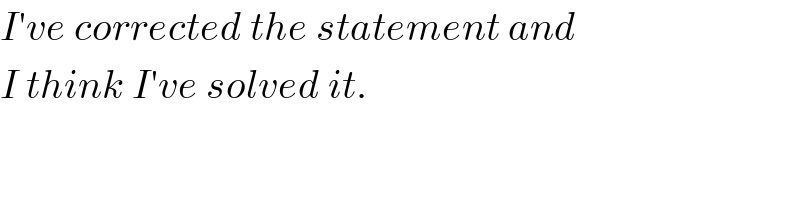
$${I}'{ve}\:{corrected}\:{the}\:{statement}\:{and} \\ $$$${I}\:{think}\:{I}'{ve}\:{solved}\:{it}.\: \\ $$
