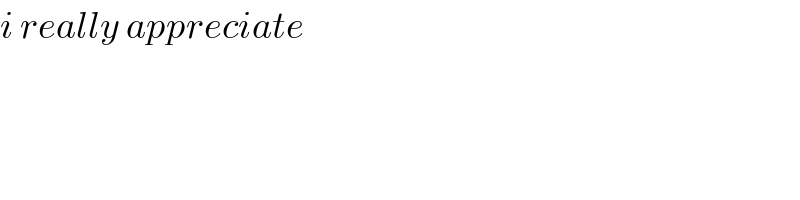Question Number 5704 by sanusihammed last updated on 24/May/16
![Show that ... Limit [((3^x − 3^(−x) )/(3^(x ) + 3^(−x) ))] = − 1 x → −∞](https://www.tinkutara.com/question/Q5704.png)
Answered by FilupSmith last updated on 24/May/16

Commented by Yozzii last updated on 24/May/16
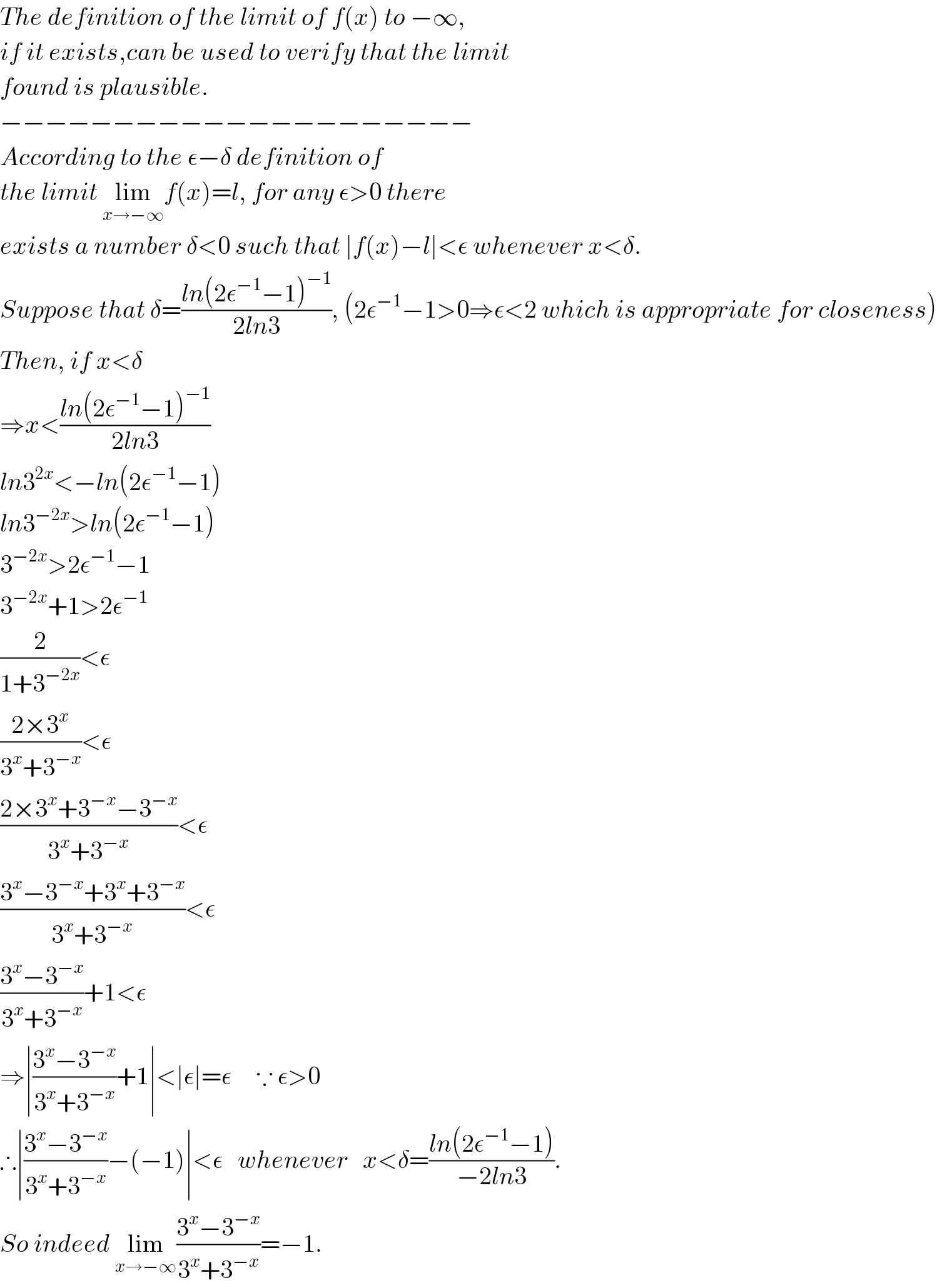
Commented by sanusihammed last updated on 24/May/16

Commented by sanusihammed last updated on 24/May/16