Menu Close

show-that-n-2-n-4-n-2-2n-1-is-converge-or-diverge-by-ussing-any-test-

Tinku Tara 0 Comments
Pin




Question Number 136559 by mohammad17 last updated on 23/Mar/21
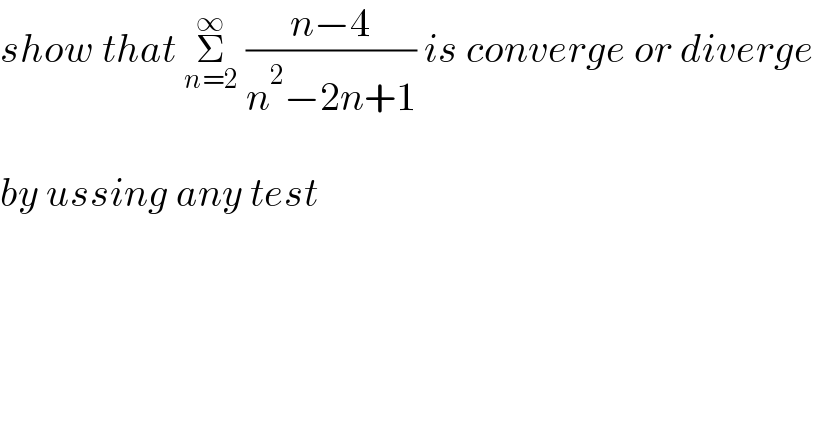
show that Σ_(n=2) ^∞ ((n−4)/(n^2 −2n+1)) is converge or diverge by ussing any test
$${show}\:{that}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:{is}\:{converge}\:{or}\:{diverge}\: \\ $$$$ \\ $$$${by}\:{ussing}\:{any}\:{test} \\ $$
Commented by mr W last updated on 23/Mar/21
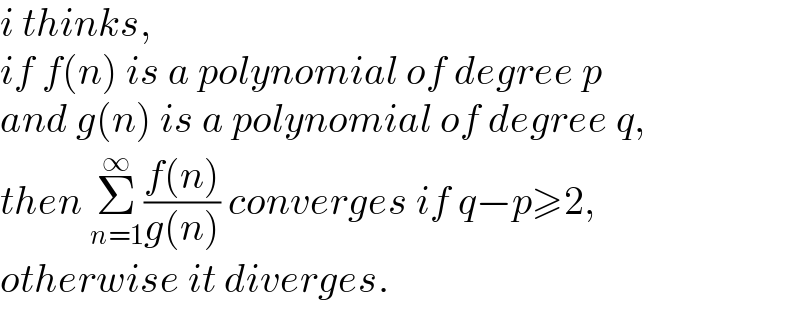
i thinks, if f(n) is a polynomial of degree p and g(n) is a polynomial of degree q, then Σ_(n=1) ^∞ ((f(n))/(g(n))) converges if q−p≥2, otherwise it diverges.
$${i}\:{thinks}, \\ $$$${if}\:{f}\left({n}\right)\:{is}\:{a}\:{polynomial}\:{of}\:{degree}\:{p} \\ $$$${and}\:{g}\left({n}\right)\:{is}\:{a}\:{polynomial}\:{of}\:{degree}\:{q}, \\ $$$${then}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{f}\left({n}\right)}{{g}\left({n}\right)}\:{converges}\:{if}\:{q}−{p}\geqslant\mathrm{2},\: \\ $$$${otherwise}\:{it}\:{diverges}. \\ $$
Answered by physicstutes last updated on 23/Mar/21
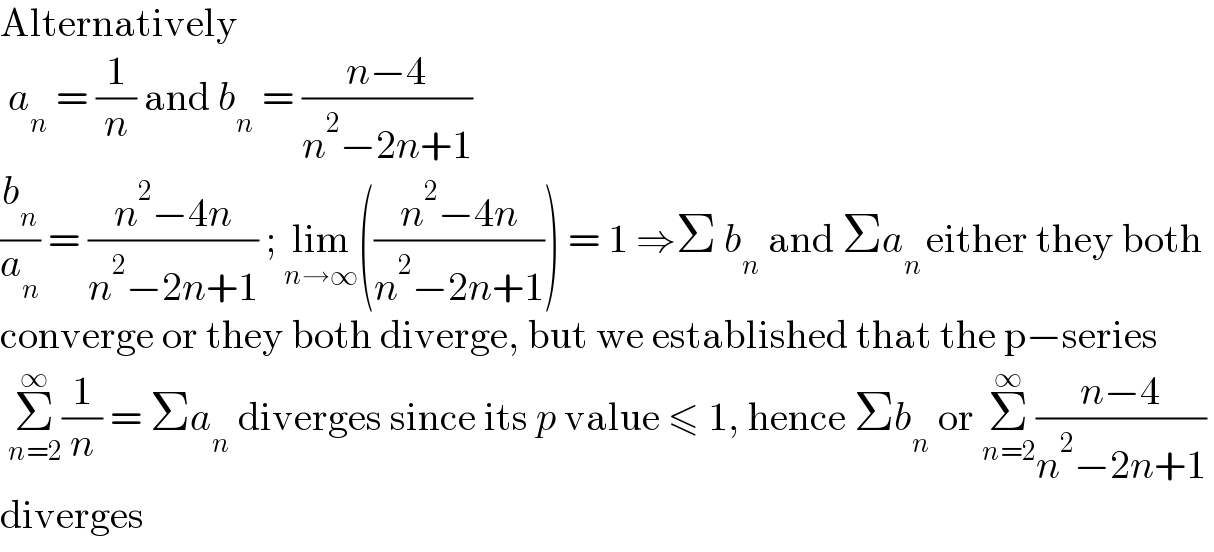
Alternatively a_n = (1/n) and b_n = ((n−4)/(n^2 −2n+1)) (b_n /a_n ) = ((n^2 −4n)/(n^2 −2n+1)) ; lim_(n→∞) (((n^2 −4n)/(n^2 −2n+1))) = 1 ⇒Σ b_n and Σa_(n ) either they both converge or they both diverge, but we established that the p−series Σ_(n=2) ^∞ (1/n) = Σa_n diverges since its p value ≤ 1, hence Σb_n or Σ_(n=2) ^∞ ((n−4)/(n^2 −2n+1)) diverges
$$\mathrm{Alternatively} \\ $$$$\:{a}_{{n}} \:=\:\frac{\mathrm{1}}{{n}}\:\mathrm{and}\:{b}_{{n}} \:=\:\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}} \\ $$$$\frac{{b}_{{n}} }{{a}_{{n}} }\:=\:\frac{{n}^{\mathrm{2}} −\mathrm{4}{n}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:;\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}^{\mathrm{2}} −\mathrm{4}{n}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\mathrm{1}\:\Rightarrow\Sigma\:{b}_{{n}} \:\mathrm{and}\:\Sigma{a}_{{n}\:} \mathrm{either}\:\mathrm{they}\:\mathrm{both} \\ $$$$\mathrm{converge}\:\mathrm{or}\:\mathrm{they}\:\mathrm{both}\:\mathrm{diverge},\:\mathrm{but}\:\mathrm{we}\:\mathrm{established}\:\mathrm{that}\:\mathrm{the}\:\mathrm{p}−\mathrm{series} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\:=\:\Sigma{a}_{{n}} \:\mathrm{diverges}\:\mathrm{since}\:\mathrm{its}\:{p}\:\mathrm{value}\:\leqslant\:\mathrm{1},\:\mathrm{hence}\:\Sigma{b}_{{n}} \:\mathrm{or}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\: \\ $$$$\mathrm{diverges} \\ $$
Answered by Olaf last updated on 23/Mar/21
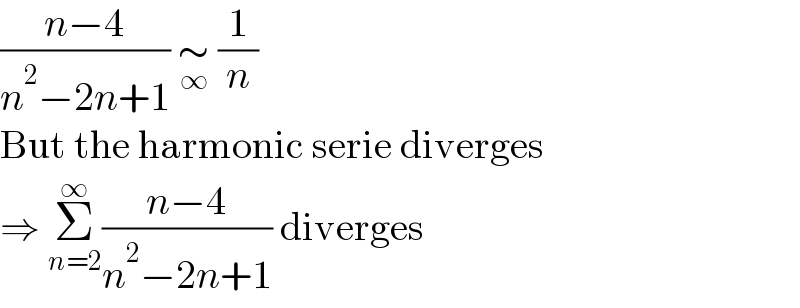
((n−4)/(n^2 −2n+1)) ∼_∞ (1/n) But the harmonic serie diverges ⇒ Σ_(n=2) ^∞ ((n−4)/(n^2 −2n+1)) diverges
$$\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:\underset{\infty} {\sim}\:\frac{\mathrm{1}}{{n}} \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{harmonic}\:\mathrm{serie}\:\mathrm{diverges} \\ $$$$\Rightarrow\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:\mathrm{diverges} \\ $$
Answered by physicstutes last updated on 23/Mar/21
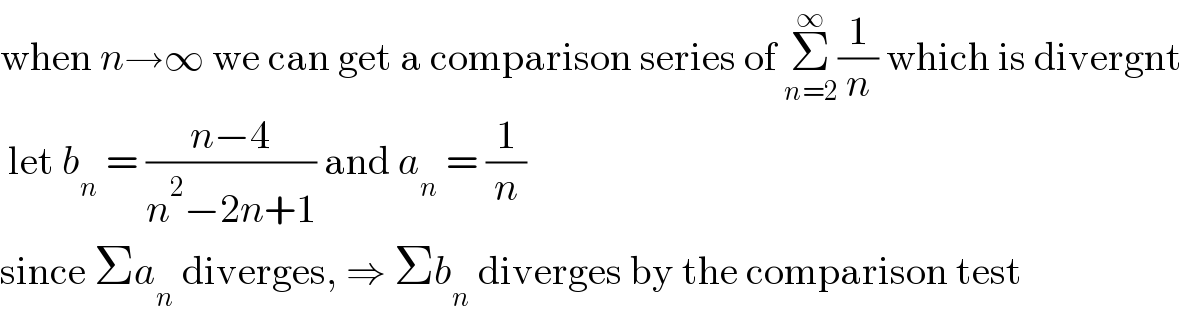
when n→∞ we can get a comparison series of Σ_(n=2) ^∞ (1/n) which is divergnt let b_n = ((n−4)/(n^2 −2n+1)) and a_n = (1/n) since Σa_n diverges, ⇒ Σb_n diverges by the comparison test
$$\mathrm{when}\:{n}\rightarrow\infty\:\mathrm{we}\:\mathrm{can}\:\mathrm{get}\:\mathrm{a}\:\mathrm{comparison}\:\mathrm{series}\:\mathrm{of}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\:\mathrm{which}\:\mathrm{is}\:\mathrm{divergnt} \\ $$$$\:\mathrm{let}\:{b}_{{n}} \:=\:\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\:\mathrm{and}\:{a}_{{n}} \:=\:\frac{\mathrm{1}}{{n}} \\ $$$$\mathrm{since}\:\Sigma{a}_{{n}} \:\mathrm{diverges},\:\Rightarrow\:\Sigma{b}_{{n}} \:\mathrm{diverges}\:\mathrm{by}\:\mathrm{the}\:\mathrm{comparison}\:\mathrm{test} \\ $$
Answered by physicstutes last updated on 23/Mar/21
another alternative Σ_(n=2) ^∞ (((n−4)/(n^2 −2n+1))) = Σ_(n=2) ^∞ [((n−4)/((n−1)^2 ))] = Σ_(n=2) ^∞ ((1/(n−1))−(3/((n−1)^2 ))) Σ_(n=2) ^∞ ((1/(n−1))) another divergent harmonic Σ_(n=2) ^∞ [(3/((n−1)^2 ))] yet another divergent one so Σ_(n=2) ^∞ (((n−4)/(n^2 −2n+1))) is divergent from all universes.
$$\mathrm{another}\:\mathrm{alternative} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\:\left[\frac{{n}−\mathrm{4}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right]\:=\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{3}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}\right)\:\mathrm{another}\:\mathrm{divergent}\:\mathrm{harmonic} \\ $$$$\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{3}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }\right]\:\mathrm{yet}\:\mathrm{another}\:\mathrm{divergent}\:\mathrm{one}\:\mathrm{so}\:\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{{n}−\mathrm{4}}{{n}^{\mathrm{2}} −\mathrm{2}{n}+\mathrm{1}}\right)\:\mathrm{is}\:\mathrm{divergent} \\ $$$$\mathrm{from}\:\mathrm{all}\:\mathrm{universes}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *