Question Number 66262 by peter frank last updated on 11/Aug/19
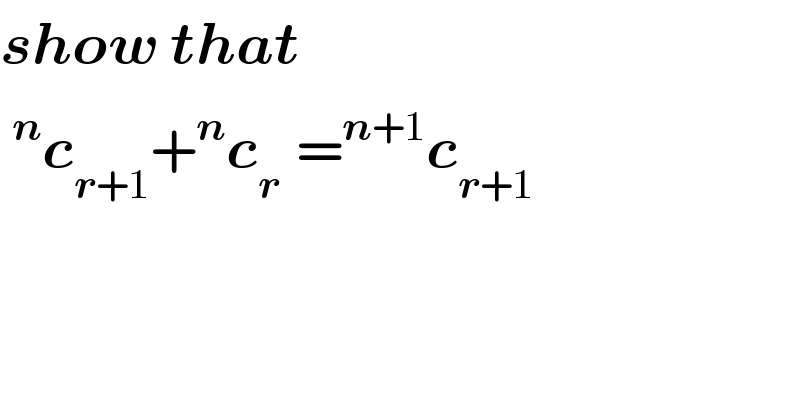
$$\boldsymbol{{show}}\:\boldsymbol{{that}}\: \\ $$$$\:^{\boldsymbol{{n}}} \boldsymbol{{c}}_{\boldsymbol{{r}}+\mathrm{1}} +^{\boldsymbol{{n}}} \boldsymbol{{c}}_{\boldsymbol{{r}}\:\:} =^{\boldsymbol{{n}}+\mathrm{1}} \boldsymbol{{c}}_{\boldsymbol{{r}}+\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 12/Aug/19
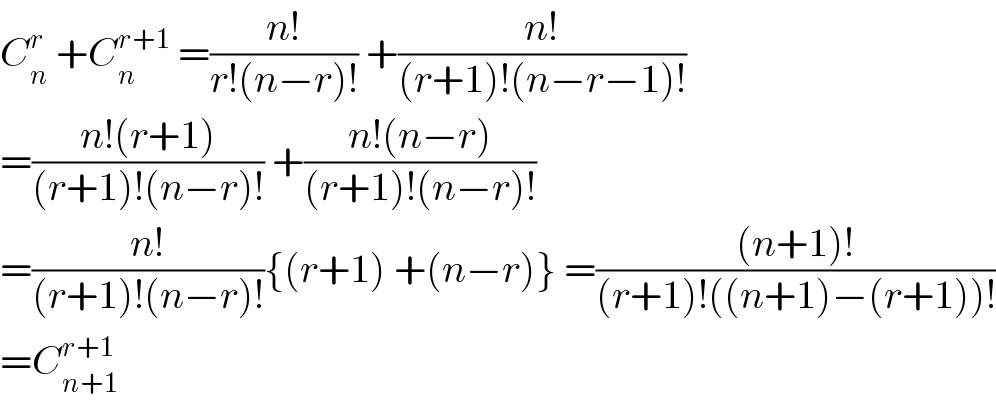
$${C}_{{n}} ^{{r}} \:+{C}_{{n}} ^{{r}+\mathrm{1}} \:=\frac{{n}!}{{r}!\left({n}−{r}\right)!}\:+\frac{{n}!}{\left({r}+\mathrm{1}\right)!\left({n}−{r}−\mathrm{1}\right)!} \\ $$$$=\frac{{n}!\left({r}+\mathrm{1}\right)}{\left({r}+\mathrm{1}\right)!\left({n}−{r}\right)!}\:+\frac{{n}!\left({n}−{r}\right)}{\left({r}+\mathrm{1}\right)!\left({n}−{r}\right)!} \\ $$$$=\frac{{n}!}{\left({r}+\mathrm{1}\right)!\left({n}−{r}\right)!}\left\{\left({r}+\mathrm{1}\right)\:+\left({n}−{r}\right)\right\}\:=\frac{\left({n}+\mathrm{1}\right)!}{\left({r}+\mathrm{1}\right)!\left(\left({n}+\mathrm{1}\right)−\left({r}+\mathrm{1}\right)\right)!} \\ $$$$={C}_{{n}+\mathrm{1}} ^{{r}+\mathrm{1}} \: \\ $$
Commented by peter frank last updated on 12/Aug/19

$${thank}\:{you} \\ $$
Commented by mathmax by abdo last updated on 12/Aug/19
$${you}\:{are}\:{welcome}. \\ $$
