Question Number 67664 by Rio Michael last updated on 29/Aug/19
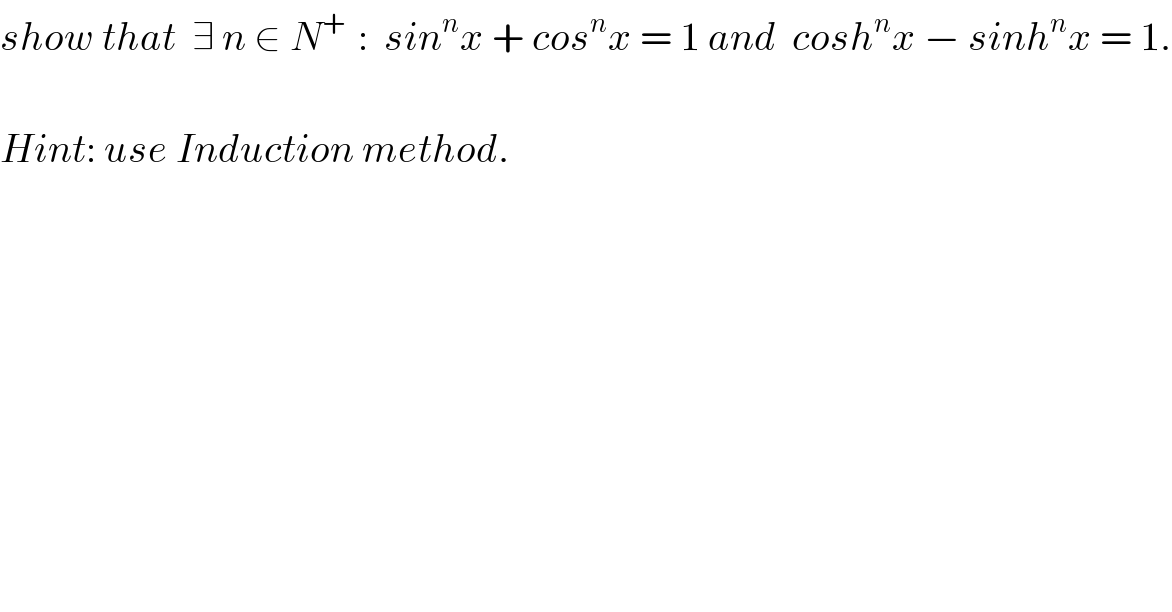
$${show}\:{that}\:\:\exists\:{n}\:\in\:{N}^{+\:} \::\:\:{sin}^{{n}} {x}\:+\:{cos}^{{n}} {x}\:=\:\mathrm{1}\:{and}\:\:{cosh}^{{n}} {x}\:−\:{sinh}^{{n}} {x}\:=\:\mathrm{1}. \\ $$$$ \\ $$$${Hint}:\:{use}\:{Induction}\:{method}. \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 30/Aug/19
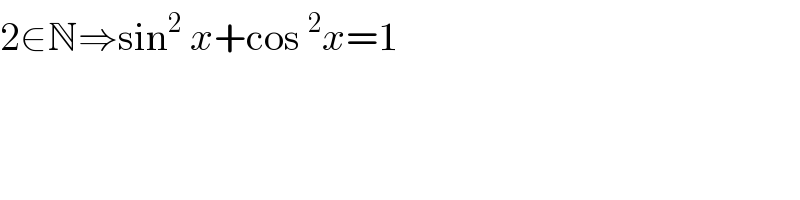
$$\mathrm{2}\in\mathbb{N}\Rightarrow\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}\:^{\mathrm{2}} {x}=\mathrm{1} \\ $$
Commented by Rio Michael last updated on 30/Aug/19
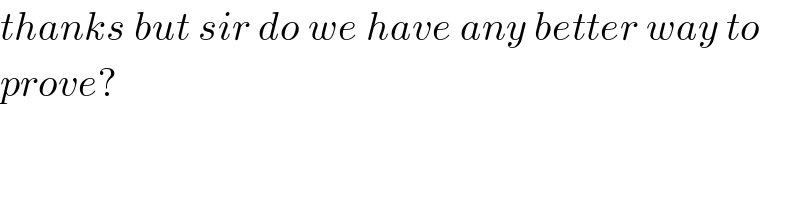
$${thanks}\:{but}\:{sir}\:{do}\:{we}\:{have}\:{any}\:{better}\:{way}\:{to} \\ $$$${prove}? \\ $$
