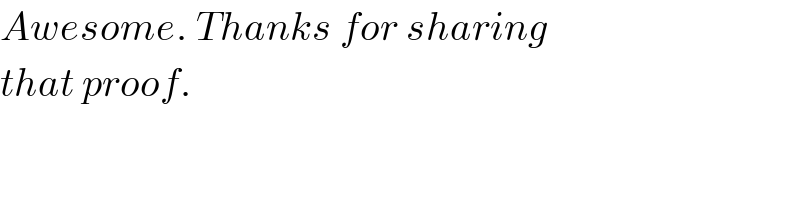Menu Close

Show-that-r-1-n-e-rx-e-x-e-nx-1-e-x-1-if-e-rx-cos-irx-isin-irx-and-x-0-Do-not-treat-as-a-GP-to-directly-obtain-the-result-

Tinku Tara 0 Comments
Pin




Question Number 1453 by 112358 last updated on 06/Aug/15
Show that Σ_(r=1) ^n e^(rx) =((e^x (e^(nx) −1))/(e^x −1)) (∗) if e^(rx) =cos(irx)−isin(irx) and x≠0 . [Do not treat (∗) as a GP to directly obtain the result.]
$${Show}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{rx}} =\frac{{e}^{{x}} \left({e}^{{nx}} −\mathrm{1}\right)}{{e}^{{x}} −\mathrm{1}}\:\:\:\:\:\:\:\left(\ast\right) \\ $$$${if}\:\:\:{e}^{{rx}} ={cos}\left({irx}\right)−{isin}\left({irx}\right)\:{and}\:{x}\neq\mathrm{0}\:. \\ $$$$\left[{Do}\:{not}\:{treat}\:\left(\ast\right)\:{as}\:{a}\:{GP}\:{to}\right. \\ $$$$\left.{directly}\:{obtain}\:{the}\:{result}.\right] \\ $$
Answered by 123456 last updated on 13/Aug/15
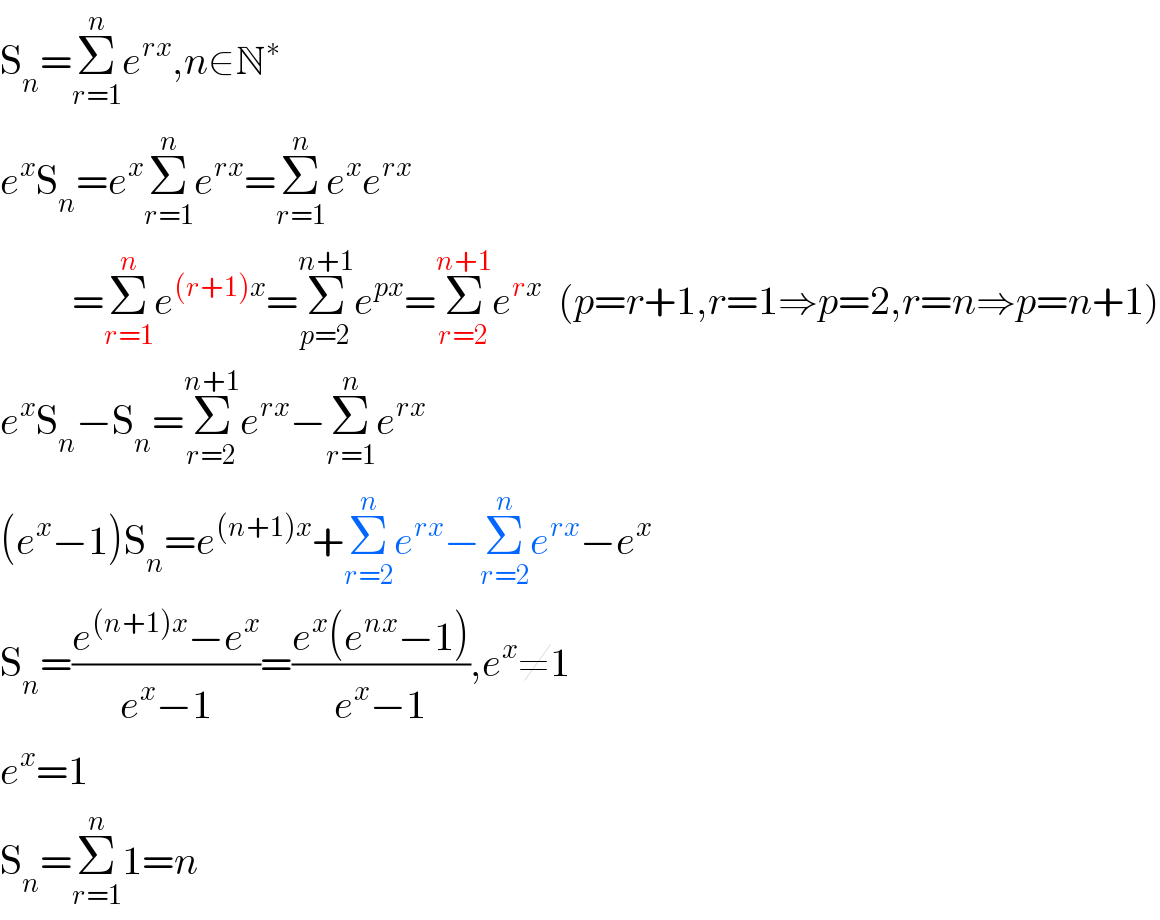
S_n =Σ_(r=1) ^n e^(rx) ,n∈N^∗ e^x S_n =e^x Σ_(r=1) ^n e^(rx) =Σ_(r=1) ^n e^x e^(rx) =Σ_(r=1) ^n e^((r+1)x) =Σ_(p=2) ^(n+1) e^(px) =Σ_(r=2) ^(n+1) e^(rx) (p=r+1,r=1⇒p=2,r=n⇒p=n+1) e^x S_n −S_n =Σ_(r=2) ^(n+1) e^(rx) −Σ_(r=1) ^n e^(rx) (e^x −1)S_n =e^((n+1)x) +Σ_(r=2) ^n e^(rx) −Σ_(r=2) ^n e^(rx) −e^x S_n =((e^((n+1)x) −e^x )/(e^x −1))=((e^x (e^(nx) −1))/(e^x −1)),e^x ≠1 e^x =1 S_n =Σ_(r=1) ^n 1=n
$$\mathrm{S}_{{n}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{rx}} ,{n}\in\mathbb{N}^{\ast} \\ $$$${e}^{{x}} \mathrm{S}_{{n}} ={e}^{{x}} \underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{rx}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{x}} {e}^{{rx}} \\ $$$$\:\:\:\:\:\:\:\:\:=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{\left({r}+\mathrm{1}\right){x}} =\underset{{p}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{px}} =\underset{{r}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{rx}} \:\:\left({p}={r}+\mathrm{1},{r}=\mathrm{1}\Rightarrow{p}=\mathrm{2},{r}={n}\Rightarrow{p}={n}+\mathrm{1}\right) \\ $$$${e}^{{x}} \mathrm{S}_{{n}} −\mathrm{S}_{{n}} =\underset{{r}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{rx}} −\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{rx}} \\ $$$$\left({e}^{{x}} −\mathrm{1}\right)\mathrm{S}_{{n}} ={e}^{\left({n}+\mathrm{1}\right){x}} +\underset{{r}=\mathrm{2}} {\overset{{n}} {\sum}}{e}^{{rx}} −\underset{{r}=\mathrm{2}} {\overset{{n}} {\sum}}{e}^{{rx}} −{e}^{{x}} \\ $$$$\mathrm{S}_{{n}} =\frac{{e}^{\left({n}+\mathrm{1}\right){x}} −{e}^{{x}} }{{e}^{{x}} −\mathrm{1}}=\frac{{e}^{{x}} \left({e}^{{nx}} −\mathrm{1}\right)}{{e}^{{x}} −\mathrm{1}},{e}^{{x}} \neq\mathrm{1} \\ $$$${e}^{{x}} =\mathrm{1} \\ $$$$\mathrm{S}_{{n}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}={n} \\ $$
Commented by 112358 last updated on 06/Aug/15
I appreciate your approach.
$${I}\:{appreciate}\:{your}\:{approach}.\: \\ $$
Commented by Rasheed Ahmad last updated on 13/Aug/15
Σ_(r=1) ^n e^((r+1)x) =Σ_(r=2) ^(n+1) e^(rx) (How? pl explain, I am asking for learning. Question should not be treated as an objection.)
$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{\left({r}+\mathrm{1}\right){x}} =\underset{{r}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{rx}} \:\: \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{How}}?\:\boldsymbol{\mathrm{pl}}\:\boldsymbol{\mathrm{explain}},\:\boldsymbol{\mathrm{I}}\:\boldsymbol{\mathrm{am}}\:\boldsymbol{\mathrm{asking}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right. \\ $$$$\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{learning}}.\:\boldsymbol{\mathrm{Question}}\:\boldsymbol{\mathrm{should}}\:\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{be}}\: \\ $$$$\left.\boldsymbol{\mathrm{treated}}\:\boldsymbol{\mathrm{as}}\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{objection}}.\right) \\ $$$$ \\ $$
Commented by 112358 last updated on 13/Aug/15
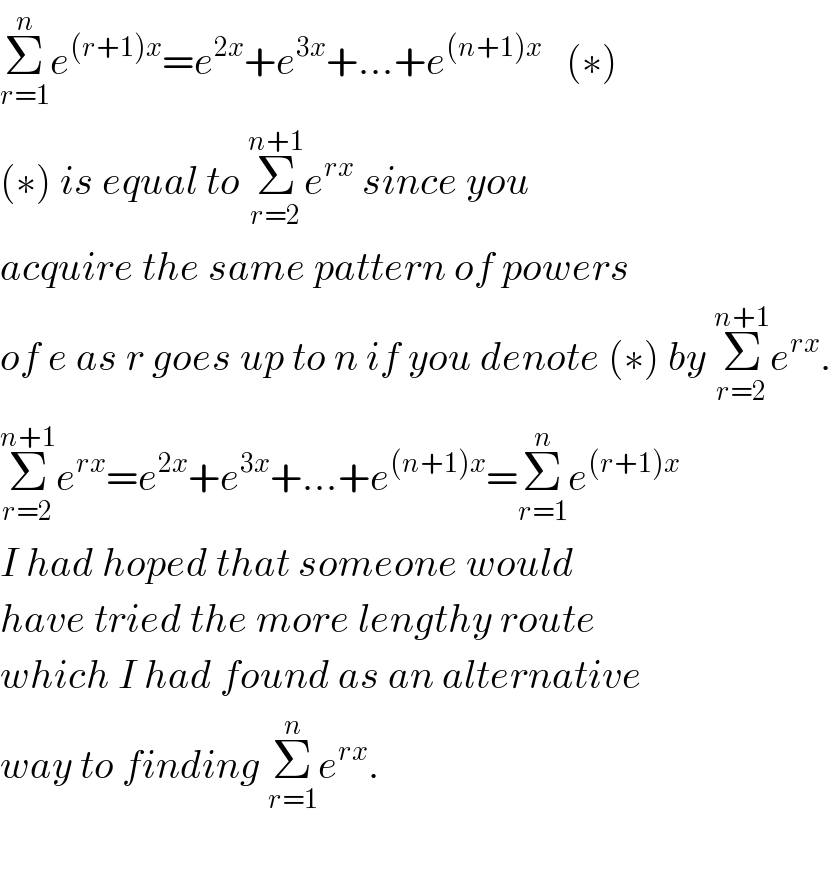
Σ_(r=1) ^n e^((r+1)x) =e^(2x) +e^(3x) +...+e^((n+1)x) (∗) (∗) is equal to Σ_(r=2) ^(n+1) e^(rx) since you acquire the same pattern of powers of e as r goes up to n if you denote (∗) by Σ_(r=2) ^(n+1) e^(rx) . Σ_(r=2) ^(n+1) e^(rx) =e^(2x) +e^(3x) +...+e^((n+1)x) =Σ_(r=1) ^n e^((r+1)x) I had hoped that someone would have tried the more lengthy route which I had found as an alternative way to finding Σ_(r=1) ^n e^(rx) .
$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{\left({r}+\mathrm{1}\right){x}} ={e}^{\mathrm{2}{x}} +{e}^{\mathrm{3}{x}} +…+{e}^{\left({n}+\mathrm{1}\right){x}} \:\:\:\left(\ast\right) \\ $$$$\left(\ast\right)\:{is}\:{equal}\:{to}\:\underset{{r}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{rx}} \:{since}\:{you} \\ $$$${acquire}\:{the}\:{same}\:{pattern}\:{of}\:{powers} \\ $$$${of}\:{e}\:{as}\:{r}\:{goes}\:{up}\:{to}\:{n}\:{if}\:{you}\:{denote}\:\left(\ast\right)\:{by}\:\underset{{r}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{rx}} . \\ $$$$\underset{{r}=\mathrm{2}} {\overset{{n}+\mathrm{1}} {\sum}}{e}^{{rx}} ={e}^{\mathrm{2}{x}} +{e}^{\mathrm{3}{x}} +…+{e}^{\left({n}+\mathrm{1}\right){x}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{\left({r}+\mathrm{1}\right){x}} \\ $$$${I}\:{had}\:{hoped}\:{that}\:{someone}\:{would} \\ $$$${have}\:{tried}\:{the}\:{more}\:{lengthy}\:{route} \\ $$$${which}\:{I}\:{had}\:{found}\:{as}\:{an}\:{alternative} \\ $$$${way}\:{to}\:{finding}\:\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{rx}} . \\ $$$$ \\ $$
Commented by Rasheed Ahmad last updated on 13/Aug/15
THANKS For explaining! Your approach is realy appreciable!
$$\boldsymbol{\mathrm{THANKS}}\:\boldsymbol{\mathrm{For}}\:\boldsymbol{\mathrm{explaining}}! \\ $$$$\mathrm{Y}\boldsymbol{\mathrm{our}}\:\boldsymbol{\mathrm{approach}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{realy}}\:\boldsymbol{\mathrm{appreciable}}! \\ $$
Commented by 123456 last updated on 13/Aug/15
L=lim_(x→0) ((e^((n+1)x) −e^x )/(e^x −1))=lim_(x→0) ((e^x (e^(nx) −1))/(e^x −1)) L=lim_(x→0) e^x lim_(x→0) ((e^(nx) −1)/(e^x −1))=lim_(x→0) ((e^(nx) −1)/(e^x −1)) lim_(x→0) ((e^x −1)/x)=1 L=lim_(x→0) ((e^(nx) −1)/(e^x −1))=lim_(x→0) ((((nx)/(nx))(e^(nx) −1))/((x/x)(e^x −1))) L=lim_(x→0) ((nx((e^(nx) −1)/(nx)))/(x((e^x −1)/x)))=nlim_(x→0) (((e^(nx) −1)/(nx))/((e^x −1)/x)) L=n((lim_(x→0) ((e^(nx) −1)/(nx)))/(lim_(x→0) ((e^x −1)/x)))(y=nx,x→0≡y→0) L=nlim_(y→0) ((e^y −1)/y)=n
$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\left({n}+\mathrm{1}\right){x}} −{e}^{{x}} }{{e}^{{x}} −\mathrm{1}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} \left({e}^{{nx}} −\mathrm{1}\right)}{{e}^{{x}} −\mathrm{1}} \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{{x}} \underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{nx}} −\mathrm{1}}{{e}^{{x}} −\mathrm{1}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{nx}} −\mathrm{1}}{{e}^{{x}} −\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} −\mathrm{1}}{{x}}=\mathrm{1} \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{nx}} −\mathrm{1}}{{e}^{{x}} −\mathrm{1}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{nx}}{{nx}}\left({e}^{{nx}} −\mathrm{1}\right)}{\frac{{x}}{{x}}\left({e}^{{x}} −\mathrm{1}\right)} \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{nx}\frac{{e}^{{nx}} −\mathrm{1}}{{nx}}}{{x}\frac{{e}^{{x}} −\mathrm{1}}{{x}}}={n}\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{e}^{{nx}} −\mathrm{1}}{{nx}}}{\frac{{e}^{{x}} −\mathrm{1}}{{x}}} \\ $$$$\mathrm{L}={n}\frac{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{nx}} −\mathrm{1}}{{nx}}}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}}\left({y}={nx},{x}\rightarrow\mathrm{0}\equiv{y}\rightarrow\mathrm{0}\right) \\ $$$$\mathrm{L}={n}\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{y}} −\mathrm{1}}{{y}}={n} \\ $$
Commented by 112358 last updated on 13/Aug/15
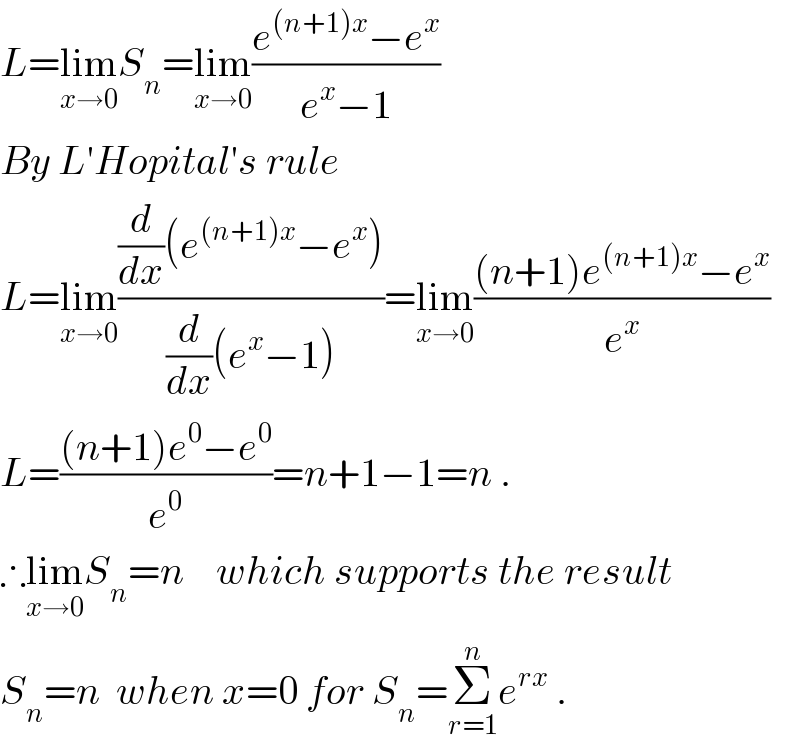
L=lim_(x→0) S_n =lim_(x→0) ((e^((n+1)x) −e^x )/(e^x −1)) By L′Hopital′s rule L=lim_(x→0) (((d/dx)(e^((n+1)x) −e^x ))/((d/dx)(e^x −1)))=lim_(x→0) (((n+1)e^((n+1)x) −e^x )/e^x ) L=(((n+1)e^0 −e^0 )/e^0 )=n+1−1=n . ∴lim_(x→0) S_n =n which supports the result S_n =n when x=0 for S_n =Σ_(r=1) ^n e^(rx) .
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{S}_{{n}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{\left({n}+\mathrm{1}\right){x}} −{e}^{{x}} }{{e}^{{x}} −\mathrm{1}} \\ $$$${By}\:{L}'{Hopital}'{s}\:{rule} \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left({e}^{\left({n}+\mathrm{1}\right){x}} −{e}^{{x}} \right)}{\frac{{d}}{{dx}}\left({e}^{{x}} −\mathrm{1}\right)}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({n}+\mathrm{1}\right){e}^{\left({n}+\mathrm{1}\right){x}} −{e}^{{x}} }{{e}^{{x}} } \\ $$$${L}=\frac{\left({n}+\mathrm{1}\right){e}^{\mathrm{0}} −{e}^{\mathrm{0}} }{{e}^{\mathrm{0}} }={n}+\mathrm{1}−\mathrm{1}={n}\:. \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{S}_{{n}} ={n}\:\:\:\:{which}\:{supports}\:{the}\:{result} \\ $$$${S}_{{n}} ={n}\:\:{when}\:{x}=\mathrm{0}\:{for}\:{S}_{{n}} =\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}{e}^{{rx}} \:. \\ $$
Commented by 112358 last updated on 13/Aug/15
I see. Good alternative approach. How may one show that lim_(x→0) ((e^x −1)/x)=1 ?
$${I}\:{see}.\:{Good}\:{alternative}\:{approach}. \\ $$$${How}\:{may}\:{one}\:{show}\:{that}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}=\mathrm{1}\:? \\ $$
Commented by 123456 last updated on 14/Aug/15
F(a)=lim_(x→0) ((a^x −1)/x),a>0,a≠1 x=log_a (t+1) x→0≡t→0 F(a)=lim_(t→0) ((a^(log_a (t+1)) −1)/(log_a (t+1))) F(a)=lim_(t→0) (t/(log_a (t+1))) [log_a (t+1)=((ln (t+1))/(ln a))] F(a)=lim_(t→0) ((tln a)/(ln (t+1)))=lim_(t→0) ((ln a)/((1/t)ln(1+t))) F(a)=((ln a)/(lim_(t→0) ln(1+t)^(1/t) ))=((ln a)/(ln lim_(t→0) (1+t)^(1/t) )) fundamental limit:lim_(t→0) (1+t)^(1/t) =e F(a)=((ln a)/(ln e))=ln a a=e F(e)=1
$$\mathrm{F}\left({a}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}^{{x}} −\mathrm{1}}{{x}},{a}>\mathrm{0},{a}\neq\mathrm{1} \\ $$$${x}=\mathrm{log}_{{a}} \left({t}+\mathrm{1}\right) \\ $$$${x}\rightarrow\mathrm{0}\equiv{t}\rightarrow\mathrm{0} \\ $$$$\mathrm{F}\left({a}\right)=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{a}^{\mathrm{log}_{{a}} \left({t}+\mathrm{1}\right)} −\mathrm{1}}{\mathrm{log}_{{a}} \left({t}+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left({a}\right)=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{t}}{\mathrm{log}_{{a}} \left({t}+\mathrm{1}\right)}\:\:\left[\mathrm{log}_{{a}} \left({t}+\mathrm{1}\right)=\frac{\mathrm{ln}\:\left({t}+\mathrm{1}\right)}{\mathrm{ln}\:{a}}\right] \\ $$$$\mathrm{F}\left({a}\right)=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{t}\mathrm{ln}\:{a}}{\mathrm{ln}\:\left({t}+\mathrm{1}\right)}=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:{a}}{\frac{\mathrm{1}}{{t}}\mathrm{ln}\left(\mathrm{1}+{t}\right)} \\ $$$$\mathrm{F}\left({a}\right)=\frac{\mathrm{ln}\:{a}}{\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\left(\mathrm{1}+{t}\right)^{\mathrm{1}/{t}} \:}=\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{t}\right)^{\mathrm{1}/{t}} } \\ $$$$\mathrm{fundamental}\:\mathrm{limit}:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{t}\right)^{\mathrm{1}/{t}} ={e} \\ $$$$\mathrm{F}\left({a}\right)=\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{e}}=\mathrm{ln}\:{a} \\ $$$${a}={e} \\ $$$$\mathrm{F}\left({e}\right)=\mathrm{1} \\ $$
Commented by 112358 last updated on 14/Aug/15
Awesome. Thanks for sharing that proof.
$${Awesome}.\:{Thanks}\:{for}\:{sharing}\: \\ $$$${that}\:{proof}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *