Question Number 6145 by Ninik last updated on 16/Jun/16
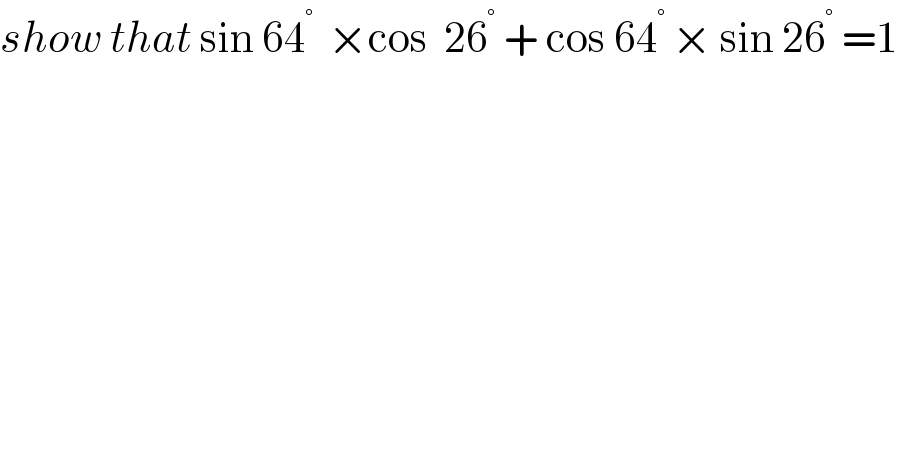
$${show}\:{that}\:\mathrm{sin}\:\mathrm{64}^{°\:} \:×\mathrm{cos}\:\:\mathrm{26}^{°} \:+\:\mathrm{cos}\:\mathrm{64}^{°\:} ×\:\mathrm{sin}\:\mathrm{26}^{°} \:=\mathrm{1}\: \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 16/Jun/16
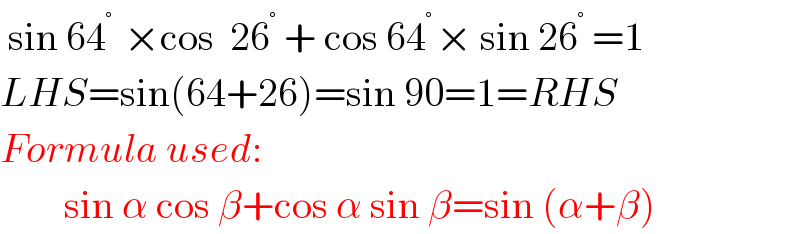
$$\:\mathrm{sin}\:\mathrm{64}^{°\:} \:×\mathrm{cos}\:\:\mathrm{26}^{°} \:+\:\mathrm{cos}\:\mathrm{64}^{°\:} ×\:\mathrm{sin}\:\mathrm{26}^{°} \:=\mathrm{1}\: \\ $$$${LHS}=\mathrm{sin}\left(\mathrm{64}+\mathrm{26}\right)=\mathrm{sin}\:\mathrm{90}=\mathrm{1}={RHS} \\ $$$${Formula}\:{used}: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta+\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta=\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$
