Question Number 8275 by lepan last updated on 05/Oct/16
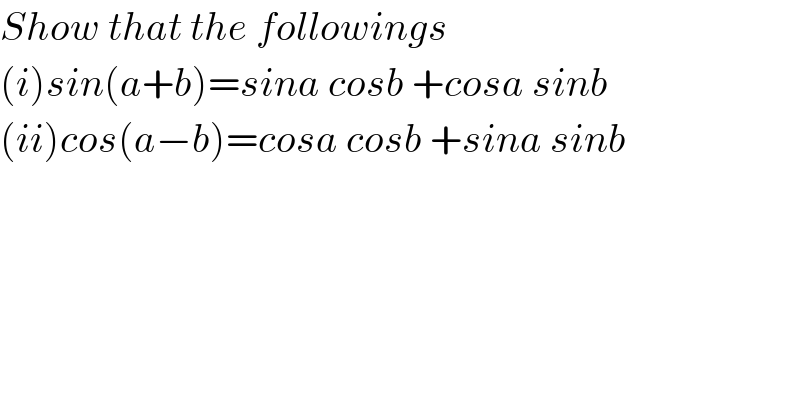
$${Show}\:{that}\:{the}\:{followings} \\ $$$$\left({i}\right){sin}\left({a}+{b}\right)={sina}\:{cosb}\:+{cosa}\:{sinb} \\ $$$$\left({ii}\right){cos}\left({a}−{b}\right)={cosa}\:{cosb}\:+{sina}\:{sinb} \\ $$$$ \\ $$
Commented by sou1618 last updated on 05/Oct/16
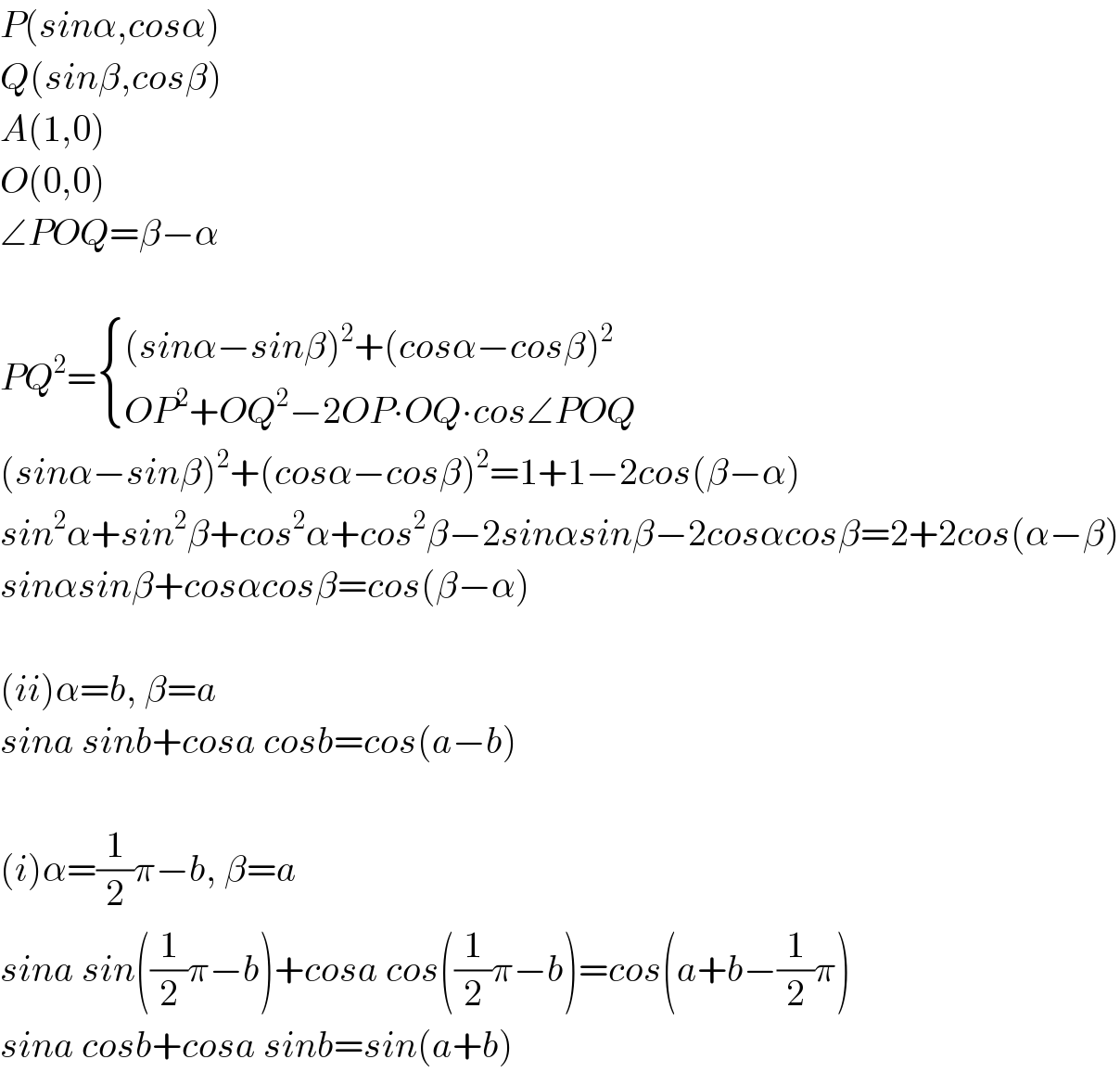
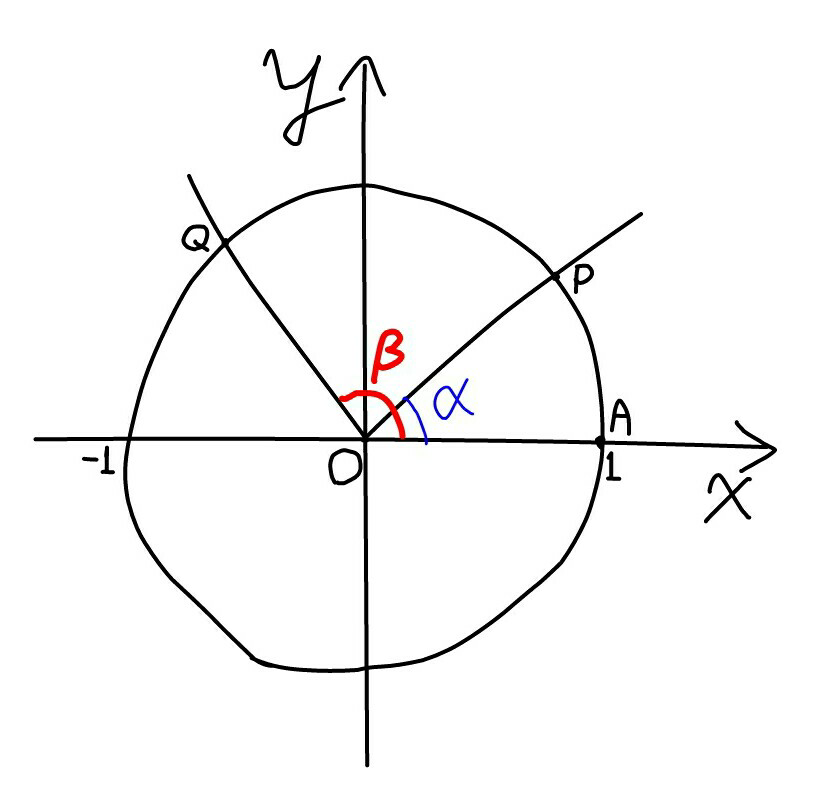
$${P}\left({sin}\alpha,{cos}\alpha\right) \\ $$$${Q}\left({sin}\beta,{cos}\beta\right) \\ $$$${A}\left(\mathrm{1},\mathrm{0}\right) \\ $$$${O}\left(\mathrm{0},\mathrm{0}\right) \\ $$$$\angle{POQ}=\beta−\alpha \\ $$$$ \\ $$$${PQ}^{\mathrm{2}} =\begin{cases}{\left({sin}\alpha−{sin}\beta\right)^{\mathrm{2}} +\left({cos}\alpha−{cos}\beta\right)^{\mathrm{2}} }\\{{OP}^{\mathrm{2}} +{OQ}^{\mathrm{2}} −\mathrm{2}{OP}\centerdot{OQ}\centerdot{cos}\angle{POQ}}\end{cases} \\ $$$$\left({sin}\alpha−{sin}\beta\right)^{\mathrm{2}} +\left({cos}\alpha−{cos}\beta\right)^{\mathrm{2}} =\mathrm{1}+\mathrm{1}−\mathrm{2}{cos}\left(\beta−\alpha\right) \\ $$$${sin}^{\mathrm{2}} \alpha+{sin}^{\mathrm{2}} \beta+{cos}^{\mathrm{2}} \alpha+{cos}^{\mathrm{2}} \beta−\mathrm{2}{sin}\alpha{sin}\beta−\mathrm{2}{cos}\alpha{cos}\beta=\mathrm{2}+\mathrm{2}{cos}\left(\alpha−\beta\right) \\ $$$${sin}\alpha{sin}\beta+{cos}\alpha{cos}\beta={cos}\left(\beta−\alpha\right) \\ $$$$ \\ $$$$\left({ii}\right)\alpha={b},\:\beta={a} \\ $$$${sina}\:{sinb}+{cosa}\:{cosb}={cos}\left({a}−{b}\right) \\ $$$$ \\ $$$$\left({i}\right)\alpha=\frac{\mathrm{1}}{\mathrm{2}}\pi−{b},\:\beta={a} \\ $$$${sina}\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\pi−{b}\right)+{cosa}\:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\pi−{b}\right)={cos}\left({a}+{b}−\frac{\mathrm{1}}{\mathrm{2}}\pi\right) \\ $$$${sina}\:{cosb}+{cosa}\:{sinb}={sin}\left({a}+{b}\right) \\ $$
Commented by sou1618 last updated on 05/Oct/16