Question Number 133445 by benjo_mathlover last updated on 22/Feb/21
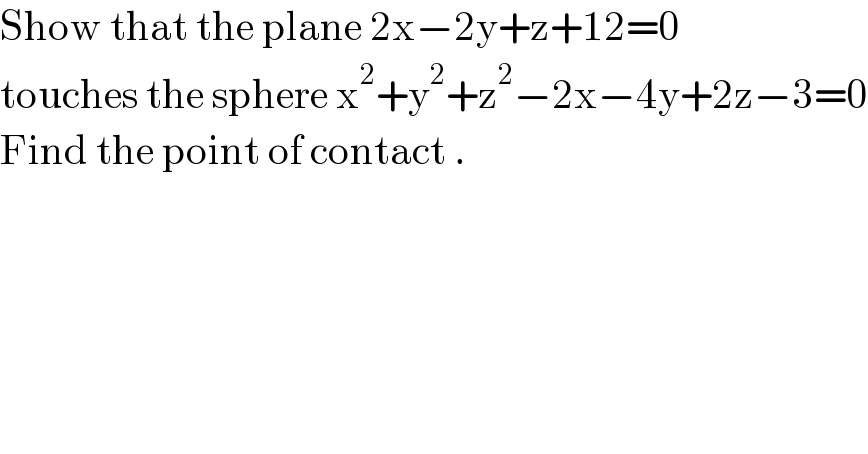
$$\mathrm{Show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{plane}\:\mathrm{2x}−\mathrm{2y}+\mathrm{z}+\mathrm{12}=\mathrm{0} \\ $$$$\mathrm{touches}\:\mathrm{the}\:\mathrm{sphere}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} −\mathrm{2x}−\mathrm{4y}+\mathrm{2z}−\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{point}\:\mathrm{of}\:\mathrm{contact}\:. \\ $$
Answered by MJS_new last updated on 22/Feb/21
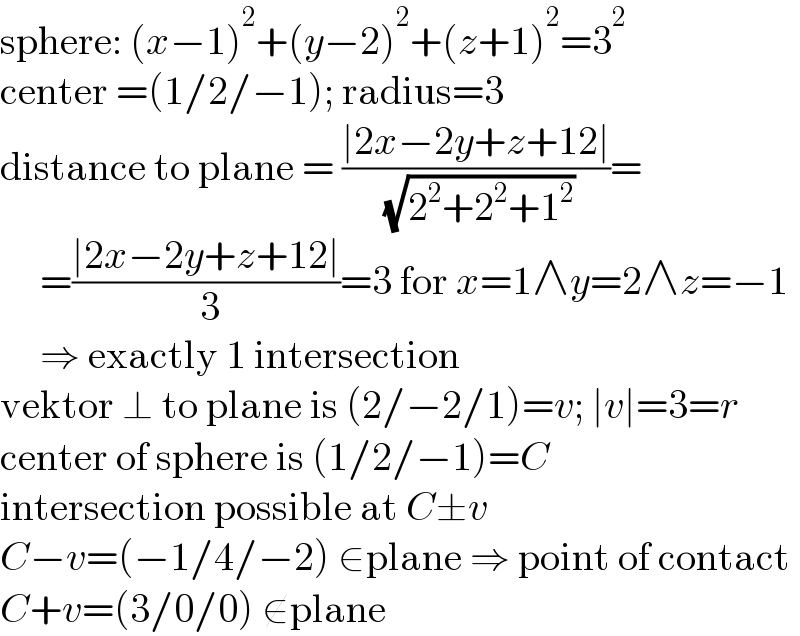
$$\mathrm{sphere}:\:\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{2}\right)^{\mathrm{2}} +\left({z}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{center}\:=\left(\mathrm{1}/\mathrm{2}/−\mathrm{1}\right);\:\mathrm{radius}=\mathrm{3} \\ $$$$\mathrm{distance}\:\mathrm{to}\:\mathrm{plane}\:=\:\frac{\mid\mathrm{2}{x}−\mathrm{2}{y}+{z}+\mathrm{12}\mid}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:=\frac{\mid\mathrm{2}{x}−\mathrm{2}{y}+{z}+\mathrm{12}\mid}{\:\mathrm{3}}=\mathrm{3}\:\mathrm{for}\:{x}=\mathrm{1}\wedge{y}=\mathrm{2}\wedge{z}=−\mathrm{1} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{intersection} \\ $$$$\mathrm{vektor}\:\bot\:\mathrm{to}\:\mathrm{plane}\:\mathrm{is}\:\left(\mathrm{2}/−\mathrm{2}/\mathrm{1}\right)={v};\:\mid{v}\mid=\mathrm{3}={r} \\ $$$$\mathrm{center}\:\mathrm{of}\:\mathrm{sphere}\:\mathrm{is}\:\left(\mathrm{1}/\mathrm{2}/−\mathrm{1}\right)={C} \\ $$$$\mathrm{intersection}\:\mathrm{possible}\:\mathrm{at}\:{C}\pm{v} \\ $$$${C}−{v}=\left(−\mathrm{1}/\mathrm{4}/−\mathrm{2}\right)\:\in\mathrm{plane}\:\Rightarrow\:\mathrm{point}\:\mathrm{of}\:\mathrm{contact} \\ $$$${C}+{v}=\left(\mathrm{3}/\mathrm{0}/\mathrm{0}\right)\:\notin\mathrm{plane} \\ $$
Commented by benjo_mathlover last updated on 22/Feb/21

$$\mathrm{thanks}\:\mathrm{prof} \\ $$
