Menu Close

show-that-the-plane-x-2y-3z-d-0-is-perpendiculr-to-each-of-the-plane-is-2x-5y-4z-1-0-and-4x-7y-3z-2-0-

Tinku Tara 0 Comments
Pin




Question Number 8150 by trapti rathaur@ gmail.com last updated on 02/Oct/16
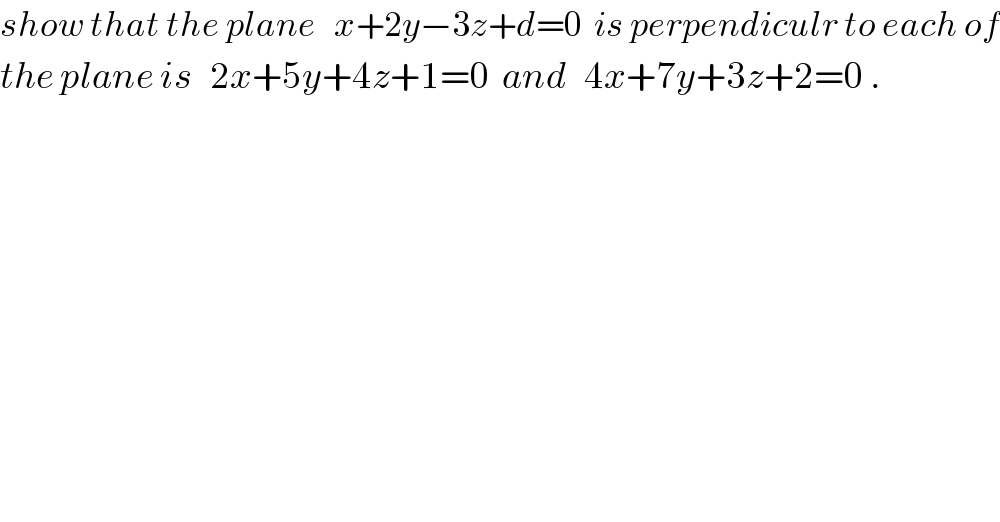
show that the plane x+2y−3z+d=0 is perpendiculr to each of the plane is 2x+5y+4z+1=0 and 4x+7y+3z+2=0 .
$${show}\:{that}\:{the}\:{plane}\:\:\:{x}+\mathrm{2}{y}−\mathrm{3}{z}+{d}=\mathrm{0}\:\:{is}\:{perpendiculr}\:{to}\:{each}\:{of} \\ $$$${the}\:{plane}\:{is}\:\:\:\mathrm{2}{x}+\mathrm{5}{y}+\mathrm{4}{z}+\mathrm{1}=\mathrm{0}\:\:{and}\:\:\:\mathrm{4}{x}+\mathrm{7}{y}+\mathrm{3}{z}+\mathrm{2}=\mathrm{0}\:.\: \\ $$
Commented by 123456 last updated on 03/Oct/16
α:x+2y−3z+d=0 β:2x+5y+4z+1=0 γ:4x+7y+3z+2=0 lets r^→ ,s^→ ,t^→ be the normal vector of α,β,γ we have r^→ =(1,2,−3) s^→ =(2,5,4) t^→ =(4,7,3) if two plan are perp, their normal vector are perp too two vector are perp if their dot product equal to 0 r^→ ∙s^→ =(1,2,−3)∙(2,5,4) =1×2+2×5−3×4 =2+10−12 =12−12 =0 r^→ ∙t^→ =(1,2,−3)∙(4,7,3) =1×4+2×7−3×3 =4+14−9 =18−9 =9≠0 s^→ ∙t^→ =(2,5,4)∙(4,7,3) =2×4+5×7+4×3 =8+35+12 =55≠0
$$\alpha:{x}+\mathrm{2}{y}−\mathrm{3}{z}+{d}=\mathrm{0} \\ $$$$\beta:\mathrm{2}{x}+\mathrm{5}{y}+\mathrm{4}{z}+\mathrm{1}=\mathrm{0} \\ $$$$\gamma:\mathrm{4}{x}+\mathrm{7}{y}+\mathrm{3}{z}+\mathrm{2}=\mathrm{0} \\ $$$$\mathrm{lets}\:\overset{\rightarrow} {{r}},\overset{\rightarrow} {{s}},\overset{\rightarrow} {{t}}\:\mathrm{be}\:\mathrm{the}\:\mathrm{normal}\:\mathrm{vector}\:\mathrm{of}\: \\ $$$$\alpha,\beta,\gamma\:\mathrm{we}\:\mathrm{have} \\ $$$$\overset{\rightarrow} {{r}}=\left(\mathrm{1},\mathrm{2},−\mathrm{3}\right) \\ $$$$\overset{\rightarrow} {{s}}=\left(\mathrm{2},\mathrm{5},\mathrm{4}\right) \\ $$$$\overset{\rightarrow} {{t}}=\left(\mathrm{4},\mathrm{7},\mathrm{3}\right) \\ $$$$\mathrm{if}\:\mathrm{two}\:\mathrm{plan}\:\mathrm{are}\:\mathrm{perp},\:\mathrm{their}\:\mathrm{normal}\:\mathrm{vector} \\ $$$$\mathrm{are}\:\mathrm{perp}\:\mathrm{too} \\ $$$$\mathrm{two}\:\mathrm{vector}\:\mathrm{are}\:\mathrm{perp}\:\mathrm{if}\:\mathrm{their}\:\mathrm{dot}\:\mathrm{product} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{0} \\ $$$$\overset{\rightarrow} {{r}}\centerdot\overset{\rightarrow} {{s}}=\left(\mathrm{1},\mathrm{2},−\mathrm{3}\right)\centerdot\left(\mathrm{2},\mathrm{5},\mathrm{4}\right) \\ $$$$=\mathrm{1}×\mathrm{2}+\mathrm{2}×\mathrm{5}−\mathrm{3}×\mathrm{4} \\ $$$$=\mathrm{2}+\mathrm{10}−\mathrm{12} \\ $$$$=\mathrm{12}−\mathrm{12} \\ $$$$=\mathrm{0} \\ $$$$\overset{\rightarrow} {{r}}\centerdot\overset{\rightarrow} {{t}}=\left(\mathrm{1},\mathrm{2},−\mathrm{3}\right)\centerdot\left(\mathrm{4},\mathrm{7},\mathrm{3}\right) \\ $$$$=\mathrm{1}×\mathrm{4}+\mathrm{2}×\mathrm{7}−\mathrm{3}×\mathrm{3} \\ $$$$=\mathrm{4}+\mathrm{14}−\mathrm{9} \\ $$$$=\mathrm{18}−\mathrm{9} \\ $$$$=\mathrm{9}\neq\mathrm{0} \\ $$$$\overset{\rightarrow} {{s}}\centerdot\overset{\rightarrow} {{t}}=\left(\mathrm{2},\mathrm{5},\mathrm{4}\right)\centerdot\left(\mathrm{4},\mathrm{7},\mathrm{3}\right) \\ $$$$=\mathrm{2}×\mathrm{4}+\mathrm{5}×\mathrm{7}+\mathrm{4}×\mathrm{3} \\ $$$$=\mathrm{8}+\mathrm{35}+\mathrm{12} \\ $$$$=\mathrm{55}\neq\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *