Menu Close

show-that-U-n-0-1-dx-1-x-x-2-x-n-converges-

Tinku Tara 0 Comments
Pin




Question Number 131590 by pticantor last updated on 06/Feb/21
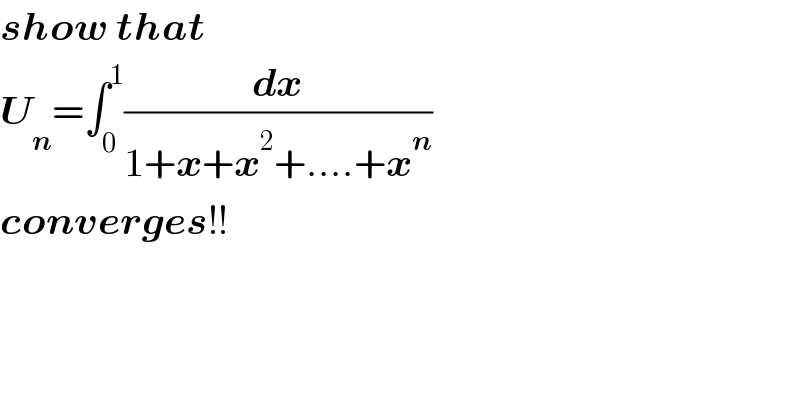
show that U_n =∫_0 ^1 (dx/(1+x+x^2 +....+x^n )) converges!!
$$\boldsymbol{{show}}\:\boldsymbol{{that}} \\ $$$$\boldsymbol{{U}}_{\boldsymbol{{n}}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{dx}}}{\mathrm{1}+\boldsymbol{{x}}+\boldsymbol{{x}}^{\mathrm{2}} +….+\boldsymbol{{x}}^{\boldsymbol{{n}}} }\: \\ $$$$\boldsymbol{{converges}}!! \\ $$
Answered by mathmax by abdo last updated on 06/Feb/21
U_n =∫_0 ^1 (((1−x))/(1−x^(n+1) ))dx ⇒lim_(n→+∞) U_n =∫_0 ^1 lim_(n→+∞) ((1−x)/(1−x^(n+1) ))dx =∫_0 ^1 (1−x)dx =[x−(x^2 /2)]_0 ^1 =1−(1/2)=(1/2) so U_n cv and U_n →(1/2)
$$\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} }\mathrm{dx}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}−\mathrm{x}^{\mathrm{n}+\mathrm{1}} }\mathrm{dx}\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:=\left[\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{so}\:\mathrm{U}_{\mathrm{n}} \mathrm{cv}\:\mathrm{and}\:\mathrm{U}_{\mathrm{n}} \rightarrow\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by pticantor last updated on 08/Feb/21
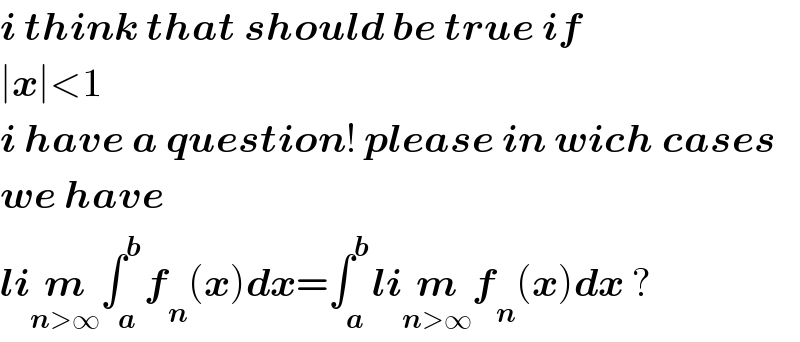
i think that should be true if ∣x∣<1 i have a question! please in wich cases we have lim_(n>∞) ∫_a ^b f_n (x)dx=∫_a ^b lim_(n>∞) f_n (x)dx ?
$$\boldsymbol{{i}}\:\boldsymbol{{think}}\:\boldsymbol{{that}}\:\boldsymbol{{should}}\:\boldsymbol{{be}}\:\boldsymbol{{true}}\:\boldsymbol{{if}} \\ $$$$\mid\boldsymbol{{x}}\mid<\mathrm{1} \\ $$$$\boldsymbol{{i}}\:\boldsymbol{{have}}\:\boldsymbol{{a}}\:\boldsymbol{{question}}!\:\boldsymbol{{please}}\:\boldsymbol{{in}}\:\boldsymbol{{wich}}\:\boldsymbol{{cases}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{have}} \\ $$$$\boldsymbol{{li}}\underset{\boldsymbol{{n}}>\infty} {\boldsymbol{{m}}}\int_{\boldsymbol{{a}}} ^{\boldsymbol{{b}}} \boldsymbol{{f}}_{\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}=\int_{\boldsymbol{{a}}} ^{\boldsymbol{{b}}} \boldsymbol{{li}}\underset{\boldsymbol{{n}}>\infty} {\boldsymbol{{m}f}}_{\boldsymbol{{n}}} \left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 06/Feb/21
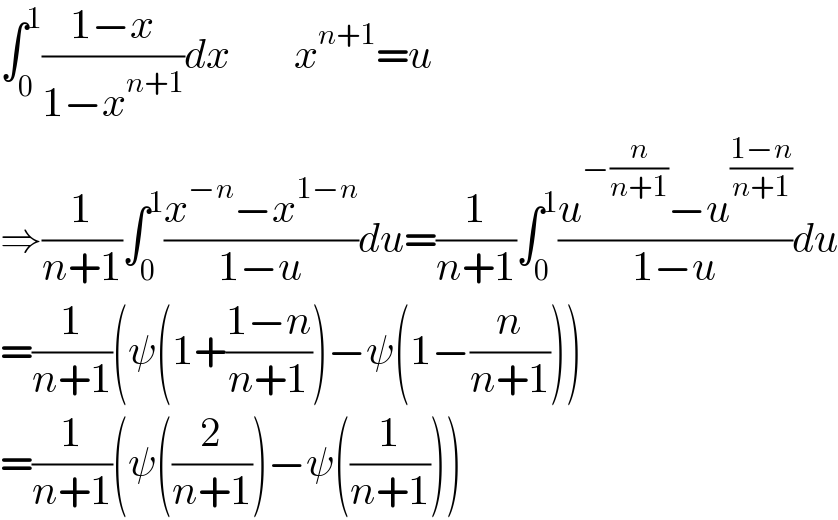
∫_0 ^1 ((1−x)/(1−x^(n+1) ))dx x^(n+1) =u ⇒(1/(n+1))∫_0 ^1 ((x^(−n) −x^(1−n) )/(1−u))du=(1/(n+1))∫_0 ^1 ((u^(−(n/(n+1))) −u^((1−n)/(n+1)) )/(1−u))du =(1/(n+1))(ψ(1+((1−n)/(n+1)))−ψ(1−(n/(n+1)))) =(1/(n+1))(ψ((2/(n+1)))−ψ((1/(n+1))))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}−{x}^{{n}+\mathrm{1}} }{dx}\:\:\:\:\:\:\:\:{x}^{{n}+\mathrm{1}} ={u} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{−{n}} −{x}^{\mathrm{1}−{n}} }{\mathrm{1}−{u}}{du}=\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{−\frac{{n}}{{n}+\mathrm{1}}} −{u}^{\frac{\mathrm{1}−{n}}{{n}+\mathrm{1}}} }{\mathrm{1}−{u}}{du} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\psi\left(\mathrm{1}+\frac{\mathrm{1}−{n}}{{n}+\mathrm{1}}\right)−\psi\left(\mathrm{1}−\frac{{n}}{{n}+\mathrm{1}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\psi\left(\frac{\mathrm{2}}{{n}+\mathrm{1}}\right)−\psi\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *