Menu Close

show-that-x-is-small-enough-for-its-cube-and-higher-power-to-be-neghected-1-x-1-x-1-x-1-2-x-2-by-putting-1-8-show-that-7-2-83-128-

Tinku Tara 0 Comments
Pin




Question Number 9576 by j.masanja06@gmail.com last updated on 18/Dec/16
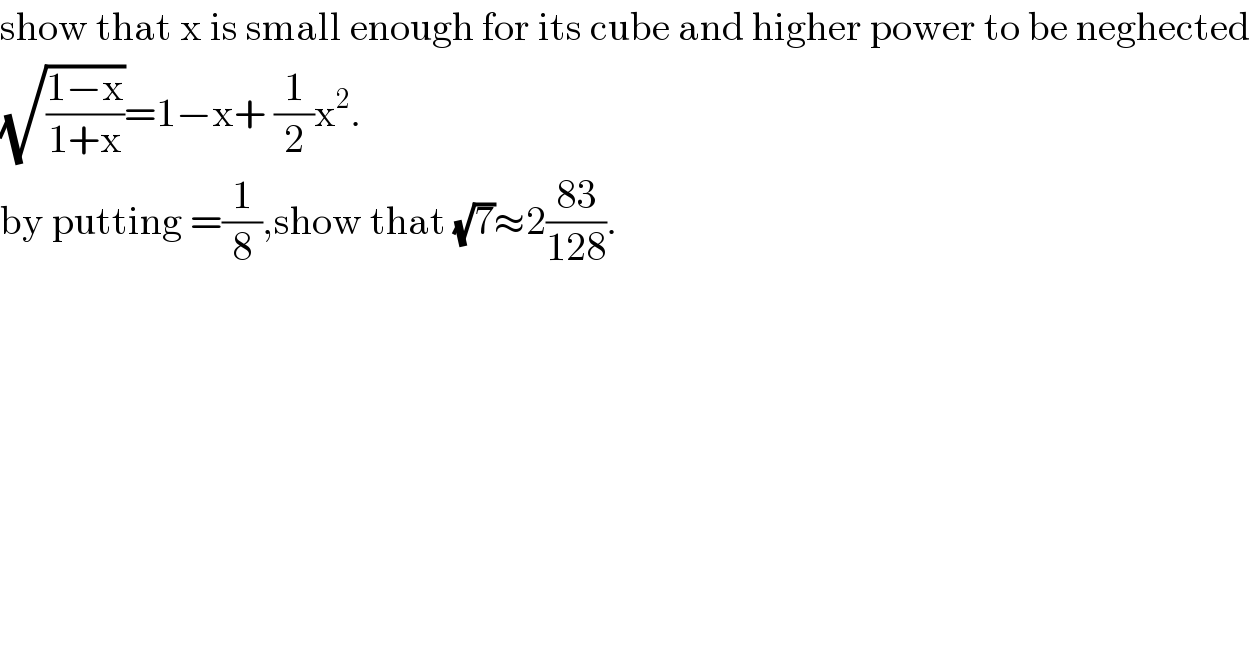
show that x is small enough for its cube and higher power to be neghected (√((1−x)/(1+x)))=1−x+ (1/2)x^2 . by putting =(1/8),show that (√7)≈2((83)/(128)).
$$\mathrm{show}\:\mathrm{that}\:\mathrm{x}\:\mathrm{is}\:\mathrm{small}\:\mathrm{enough}\:\mathrm{for}\:\mathrm{its}\:\mathrm{cube}\:\mathrm{and}\:\mathrm{higher}\:\mathrm{power}\:\mathrm{to}\:\mathrm{be}\:\mathrm{neghected} \\ $$$$\sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}=\mathrm{1}−\mathrm{x}+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} . \\ $$$$\mathrm{by}\:\mathrm{putting}\:=\frac{\mathrm{1}}{\mathrm{8}},\mathrm{show}\:\mathrm{that}\:\sqrt{\mathrm{7}}\approx\mathrm{2}\frac{\mathrm{83}}{\mathrm{128}}. \\ $$
Commented by prakash jain last updated on 20/Dec/16
From binomial theorem (1−x)^(1/2) =1−(1/2)x+(((1/2)((1/2)−1))/(2!))x^2 +...≈1−(1/2)x−(1/8)x^2 similarly (1+x)^(−1/2) ≈1−(1/2)x+(((−(1/2))(−(1/2)−1))/(2!))x^2 =1−(1/2)x+(3/8)x^2 (1−x)^(1/2) (1+x)^(−1/2) =1−x+(1/4)x^2 +(3/8)x^2 −(1/8)x^2 (1−x)^(1/2) (1+x)^(−1/2) =1−x+(1/2)x^2 put x=(1/8) to get the required result.
$$\mathrm{From}\:\mathrm{binomial}\:\mathrm{theorem} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{1}/\mathrm{2}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +…\approx\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} \\ $$$$\mathrm{similarly} \\ $$$$\left(\mathrm{1}+{x}\right)^{−\mathrm{1}/\mathrm{2}} \approx\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{3}}{\mathrm{8}}{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{1}/\mathrm{2}} \left(\mathrm{1}+{x}\right)^{−\mathrm{1}/\mathrm{2}} =\mathrm{1}−{x}+\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}−{x}\right)^{\mathrm{1}/\mathrm{2}} \left(\mathrm{1}+{x}\right)^{−\mathrm{1}/\mathrm{2}} =\mathrm{1}−{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$$\mathrm{put}\:{x}=\frac{\mathrm{1}}{\mathrm{8}}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{required}\:\mathrm{result}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *