si-g-ChineseRemainderTheorm-etermine-polynomial-p-x-such-that-p-x-8-mod-x-1-p-x-24-mod-x-3-p-x-6-mod-x-p-x-0-mod-x-2-

Question Number 67697 by Rasheed.Sindhi last updated on 30/Aug/19

$$\Cup\mathrm{si}\Cap\mathrm{g}\:\mathrm{ChineseRemainderTheorm} \\ $$$$\partial\mathrm{etermine}\:\mathrm{polynomial}\:\mathrm{p}\left(\mathrm{x}\right)\:\mathrm{such}\:\mathrm{that} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{8}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv−\mathrm{24}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{2}\right) \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 01/Sep/19

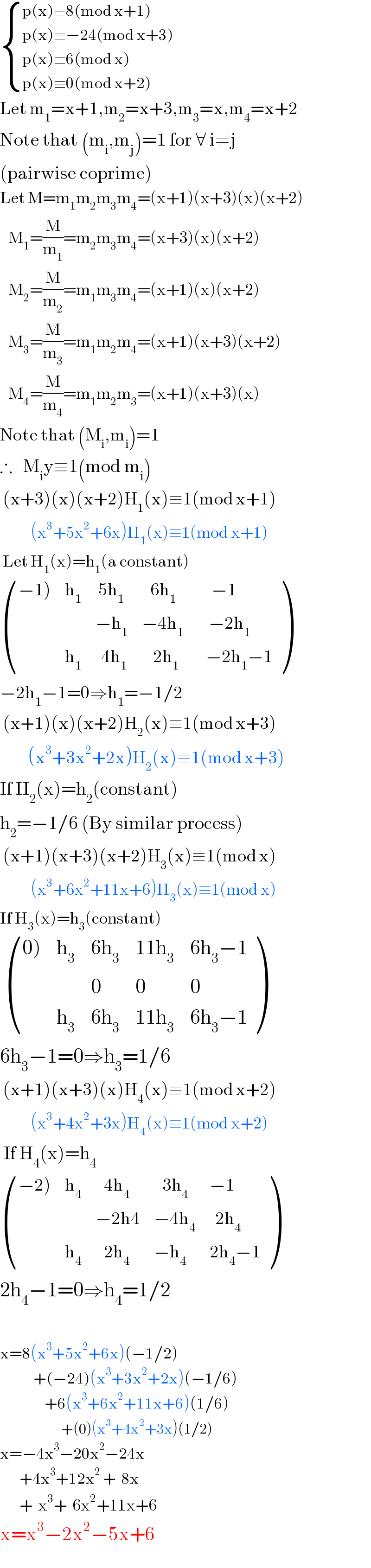
{ ((p(x)≡8(mod x+1))),((p(x)≡−24(mod x+3))),((p(x)≡6(mod x))),((p(x)≡0(mod x+2))) :} Let m_1 =x+1,m_2 =x+3,m_3 =x,m_4 =x+2 Note that (m_i ,m_j )=1 for ∀ i≠j (pairwise coprime) Let M=m_1 m_2 m_3 m_4 =(x+1)(x+3)(x)(x+2) M_1 =(M/m_1 )=m_2 m_3 m_4 =(x+3)(x)(x+2) M_2 =(M/m_2 )=m_1 m_3 m_4 =(x+1)(x)(x+2) M_3 =(M/m_3 )=m_1 m_2 m_4 =(x+1)(x+3)(x+2) M_4 =(M/m_4 )=m_1 m_2 m_3 =(x+1)(x+3)(x) Note that (M_i ,m_i )=1 ∴ M_i y≡1(mod m_i ) (x+3)(x)(x+2)H_1 (x)≡1(mod x+1) (x^3 +5x^2 +6x)H_1 (x)≡1(mod x+1) Let H_1 (x)=h_1 (a constant) (((−1)),h_1 ,( 5h_1 ),( 6h_1 ),( −1)),(,,(−h_1 ),(−4h_1 ),( −2h_1 )),(,h_1 ,( 4h_1 ),( 2h_1 ),( −2h_1 −1)) ) −2h_1 −1=0⇒h_1 =−1/2 (x+1)(x)(x+2)H_2 (x)≡1(mod x+3) (x^3 +3x^2 +2x)H_2 (x)≡1(mod x+3) If H_2 (x)=h_2 (constant) h_2 =−1/6 (By similar process) (x+1)(x+3)(x+2)H_3 (x)≡1(mod x) (x^3 +6x^2 +11x+6)H_3 (x)≡1(mod x) If H_3 (x)=h_3 (constant) (((0)),h_3 ,(6h_3 ),(11h_3 ),(6h_3 −1)),(,,0,0,0),(,h_3 ,(6h_3 ),(11h_3 ),(6h_3 −1)) ) 6h_3 −1=0⇒h_3 =1/6 (x+1)(x+3)(x)H_4 (x)≡1(mod x+2) (x^3 +4x^2 +3x)H_4 (x)≡1(mod x+2) If H_4 (x)=h_4 (((−2)),h_4 ,( 4h_4 ),( 3h_4 ),(−1)),(,,(−2h4),(−4h_4 ),( 2h_4 )),(,h_4 ,( 2h_4 ),(−h_4 ),(2h_4 −1)) ) 2h_4 −1=0⇒h_4 =1/2 x=8(x^3 +5x^2 +6x)(−1/2) +(−24)(x^3 +3x^2 +2x)(−1/6) +6(x^3 +6x^2 +11x+6)(1/6) +(0)(x^3 +4x^2 +3x)(1/2) x=−4x^3 −20x^2 −24x +4x^3 +12x^2 + 8x + x^3 + 6x^2 +11x+6 x=x^3 −2x^2 −5x+6

$$\begin{cases}{\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{8}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{1}\right)}\\{\mathrm{p}\left(\mathrm{x}\right)\equiv−\mathrm{24}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{3}\right)}\\{\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{x}\right)}\\{\mathrm{p}\left(\mathrm{x}\right)\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{2}\right)}\end{cases} \\ $$$$\mathrm{Let}\:\mathrm{m}_{\mathrm{1}} =\mathrm{x}+\mathrm{1},\mathrm{m}_{\mathrm{2}} =\mathrm{x}+\mathrm{3},\mathrm{m}_{\mathrm{3}} =\mathrm{x},\mathrm{m}_{\mathrm{4}} =\mathrm{x}+\mathrm{2} \\ $$$$\mathrm{Note}\:\mathrm{that}\:\left(\mathrm{m}_{\mathrm{i}} ,\mathrm{m}_{\mathrm{j}} \right)=\mathrm{1}\:\mathrm{for}\:\forall\:\mathrm{i}\neq\mathrm{j} \\ $$$$\left(\mathrm{pairwise}\:\mathrm{coprime}\right) \\ $$$$\mathrm{Let}\:\mathrm{M}=\mathrm{m}_{\mathrm{1}} \mathrm{m}_{\mathrm{2}} \mathrm{m}_{\mathrm{3}} \mathrm{m}_{\mathrm{4}} =\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2}\right) \\ $$$$\:\:\:\mathrm{M}_{\mathrm{1}} =\frac{\mathrm{M}}{\mathrm{m}_{\mathrm{1}} }=\mathrm{m}_{\mathrm{2}} \mathrm{m}_{\mathrm{3}} \mathrm{m}_{\mathrm{4}} =\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2}\right) \\ $$$$\:\:\:\mathrm{M}_{\mathrm{2}} =\frac{\mathrm{M}}{\mathrm{m}_{\mathrm{2}} }=\mathrm{m}_{\mathrm{1}} \mathrm{m}_{\mathrm{3}} \mathrm{m}_{\mathrm{4}} =\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2}\right) \\ $$$$\:\:\:\mathrm{M}_{\mathrm{3}} =\frac{\mathrm{M}}{\mathrm{m}_{\mathrm{3}} }=\mathrm{m}_{\mathrm{1}} \mathrm{m}_{\mathrm{2}} \mathrm{m}_{\mathrm{4}} =\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right) \\ $$$$\:\:\:\mathrm{M}_{\mathrm{4}} =\frac{\mathrm{M}}{\mathrm{m}_{\mathrm{4}} }=\mathrm{m}_{\mathrm{1}} \mathrm{m}_{\mathrm{2}} \mathrm{m}_{\mathrm{3}} =\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}\right) \\ $$$$\mathrm{Note}\:\mathrm{that}\:\left(\mathrm{M}_{\mathrm{i}} ,\mathrm{m}_{\mathrm{i}} \right)=\mathrm{1} \\ $$$$\therefore\:\:\:\mathrm{M}_{\mathrm{i}} \mathrm{y}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{m}_{\mathrm{i}} \right) \\ $$$$\:\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2}\right)\mathrm{H}_{\mathrm{1}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}^{\mathrm{3}} +\mathrm{5x}^{\mathrm{2}} +\mathrm{6x}\right)\mathrm{H}_{\mathrm{1}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{1}\right) \\ $$$$\:\mathrm{Let}\:\mathrm{H}_{\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{h}_{\mathrm{1}} \left(\mathrm{a}\:\mathrm{constant}\right) \\ $$$$\begin{pmatrix}{\left.−\mathrm{1}\right)}&{\mathrm{h}_{\mathrm{1}} }&{\:\mathrm{5h}_{\mathrm{1}} }&{\:\:\:\mathrm{6h}_{\mathrm{1}} }&{\:\:\:\:\:−\mathrm{1}}\\{}&{}&{−\mathrm{h}_{\mathrm{1}} }&{−\mathrm{4h}_{\mathrm{1}} }&{\:\:\:\:−\mathrm{2h}_{\mathrm{1}} }\\{}&{\mathrm{h}_{\mathrm{1}} }&{\:\:\mathrm{4h}_{\mathrm{1}} }&{\:\:\:\:\mathrm{2h}_{\mathrm{1}} }&{\:\:\:−\mathrm{2h}_{\mathrm{1}} −\mathrm{1}}\end{pmatrix}\: \\ $$$$−\mathrm{2h}_{\mathrm{1}} −\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{h}_{\mathrm{1}} =−\mathrm{1}/\mathrm{2} \\ $$$$\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}\right)\left(\mathrm{x}+\mathrm{2}\right)\mathrm{H}_{\mathrm{2}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}\right)\mathrm{H}_{\mathrm{2}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{3}\right) \\ $$$$\mathrm{If}\:\mathrm{H}_{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{h}_{\mathrm{2}} \left(\mathrm{constant}\right) \\ $$$$\mathrm{h}_{\mathrm{2}} =−\mathrm{1}/\mathrm{6}\:\left(\mathrm{By}\:\mathrm{similar}\:\mathrm{process}\right) \\ $$$$\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}+\mathrm{2}\right)\mathrm{H}_{\mathrm{3}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{11x}+\mathrm{6}\right)\mathrm{H}_{\mathrm{3}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}\right) \\ $$$$\mathrm{If}\:\mathrm{H}_{\mathrm{3}} \left(\mathrm{x}\right)=\mathrm{h}_{\mathrm{3}} \left(\mathrm{constant}\right) \\ $$$$\:\begin{pmatrix}{\left.\mathrm{0}\right)}&{\mathrm{h}_{\mathrm{3}} }&{\mathrm{6h}_{\mathrm{3}} }&{\mathrm{11h}_{\mathrm{3}} }&{\mathrm{6h}_{\mathrm{3}} −\mathrm{1}}\\{}&{}&{\mathrm{0}}&{\mathrm{0}}&{\mathrm{0}}\\{}&{\mathrm{h}_{\mathrm{3}} }&{\mathrm{6h}_{\mathrm{3}} }&{\mathrm{11h}_{\mathrm{3}} }&{\mathrm{6h}_{\mathrm{3}} −\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{6h}_{\mathrm{3}} −\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{h}_{\mathrm{3}} =\mathrm{1}/\mathrm{6} \\ $$$$\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{x}\right)\mathrm{H}_{\mathrm{4}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{3x}\right)\mathrm{H}_{\mathrm{4}} \left(\mathrm{x}\right)\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{x}+\mathrm{2}\right) \\ $$$$\:\mathrm{If}\:\mathrm{H}_{\mathrm{4}} \left(\mathrm{x}\right)=\mathrm{h}_{\mathrm{4}} \\ $$$$\begin{pmatrix}{\left.−\mathrm{2}\right)}&{\mathrm{h}_{\mathrm{4}} }&{\:\:\:\mathrm{4h}_{\mathrm{4}} }&{\:\:\:\mathrm{3h}_{\mathrm{4}} }&{−\mathrm{1}}\\{}&{}&{−\mathrm{2h4}}&{−\mathrm{4h}_{\mathrm{4}} }&{\:\:\mathrm{2h}_{\mathrm{4}} }\\{}&{\mathrm{h}_{\mathrm{4}} }&{\:\:\:\mathrm{2h}_{\mathrm{4}} }&{−\mathrm{h}_{\mathrm{4}} }&{\mathrm{2h}_{\mathrm{4}} −\mathrm{1}}\end{pmatrix} \\ $$$$\mathrm{2h}_{\mathrm{4}} −\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{h}_{\mathrm{4}} =\mathrm{1}/\mathrm{2} \\ $$$$ \\ $$$$\mathrm{x}=\mathrm{8}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{5x}^{\mathrm{2}} +\mathrm{6x}\right)\left(−\mathrm{1}/\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:+\left(−\mathrm{24}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} +\mathrm{2x}\right)\left(−\mathrm{1}/\mathrm{6}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{6}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{6x}^{\mathrm{2}} +\mathrm{11x}+\mathrm{6}\right)\left(\mathrm{1}/\mathrm{6}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{0}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{4x}^{\mathrm{2}} +\mathrm{3x}\right)\left(\mathrm{1}/\mathrm{2}\right) \\ $$$$\mathrm{x}=−\mathrm{4x}^{\mathrm{3}} −\mathrm{20x}^{\mathrm{2}} −\mathrm{24x} \\ $$$$\:\:\:\:\:\:\:+\mathrm{4x}^{\mathrm{3}} +\mathrm{12x}^{\mathrm{2}} \:+\:\:\mathrm{8x} \\ $$$$\:\:\:\:\:\:\:+\:\:\mathrm{x}^{\mathrm{3}} +\:\:\mathrm{6x}^{\mathrm{2}} +\mathrm{11x}+\mathrm{6} \\ $$$$\mathrm{x}=\mathrm{x}^{\mathrm{3}} −\mathrm{2x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6} \\ $$

Commented by Prithwish sen last updated on 02/Sep/19