Question Number 65983 by Rio Michael last updated on 07/Aug/19
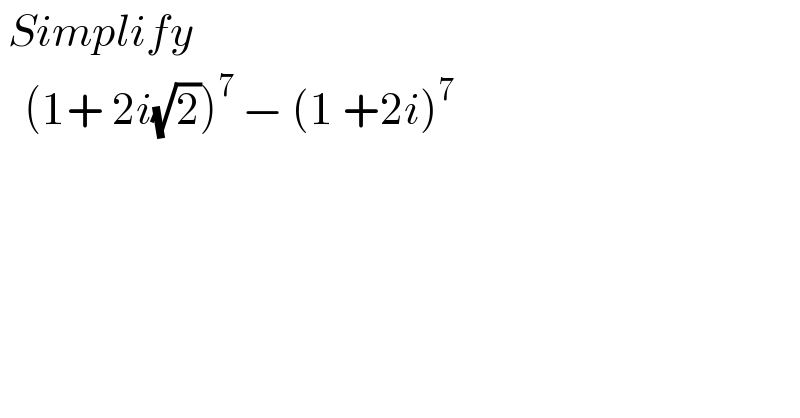
$$\:{Simplify}\: \\ $$$$\:\:\:\left(\mathrm{1}+\:\mathrm{2}{i}\sqrt{\mathrm{2}}\right)^{\mathrm{7}} \:−\:\left(\mathrm{1}\:+\mathrm{2}{i}\right)^{\mathrm{7}} \\ $$
Commented by Rio Michael last updated on 17/Aug/19
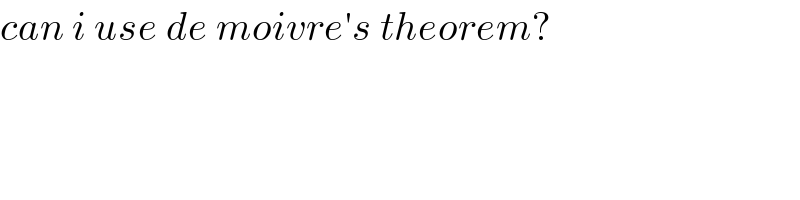
$${can}\:{i}\:{use}\:{de}\:{moivre}'{s}\:{theorem}? \\ $$
Answered by MJS last updated on 07/Aug/19
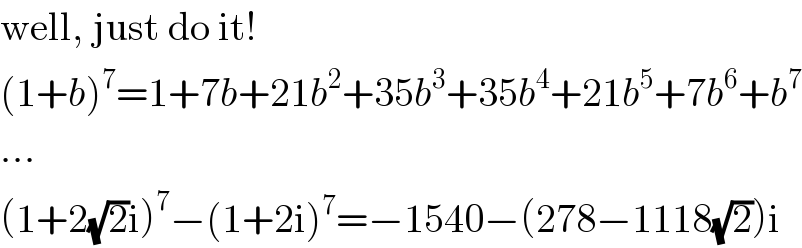
$$\mathrm{well},\:\mathrm{just}\:\mathrm{do}\:\mathrm{it}! \\ $$$$\left(\mathrm{1}+{b}\right)^{\mathrm{7}} =\mathrm{1}+\mathrm{7}{b}+\mathrm{21}{b}^{\mathrm{2}} +\mathrm{35}{b}^{\mathrm{3}} +\mathrm{35}{b}^{\mathrm{4}} +\mathrm{21}{b}^{\mathrm{5}} +\mathrm{7}{b}^{\mathrm{6}} +{b}^{\mathrm{7}} \\ $$$$… \\ $$$$\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\mathrm{i}\right)^{\mathrm{7}} −\left(\mathrm{1}+\mathrm{2i}\right)^{\mathrm{7}} =−\mathrm{1540}−\left(\mathrm{278}−\mathrm{1118}\sqrt{\mathrm{2}}\right)\mathrm{i} \\ $$
