Menu Close

simplify-A-n-2-i-5-n-2-i-5-n-and-B-n-2-i-5-n-2-i-5-n-

Tinku Tara
Pin




Question Number 65918 by mathmax by abdo last updated on 05/Aug/19
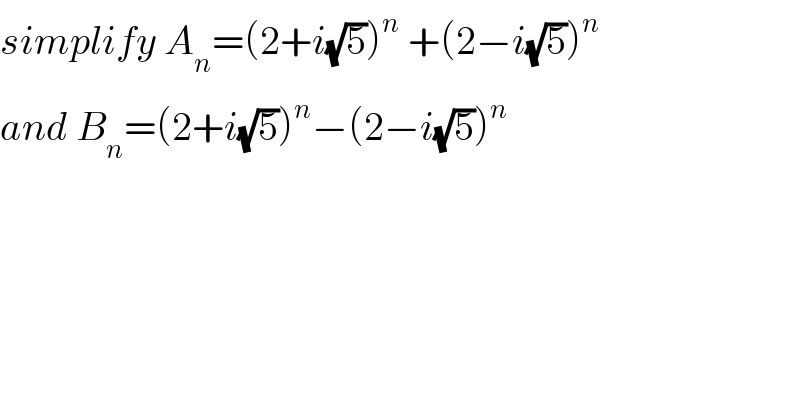
simplify A_n =(2+i(√5))^n +(2−i(√5))^n and B_n =(2+i(√5))^n −(2−i(√5))^n
$${simplify}\:{A}_{{n}} =\left(\mathrm{2}+{i}\sqrt{\mathrm{5}}\right)^{{n}} \:+\left(\mathrm{2}−{i}\sqrt{\mathrm{5}}\right)^{{n}} \\ $$$${and}\:{B}_{{n}} =\left(\mathrm{2}+{i}\sqrt{\mathrm{5}}\right)^{{n}} −\left(\mathrm{2}−{i}\sqrt{\mathrm{5}}\right)^{{n}} \\ $$
Commented by mathmax by abdo last updated on 06/Aug/19
we have ∣2+i(√5)∣ =(√(2^2 +((√5))^2 ))=(√(4+5))=3 ⇒ 2+i(√5)=3((2/3) +i((√5)/3)) =3 e^(iarctan(((√5)/2))) ⇒(2+i(√5))^n =3^n e^(inarctan(((√5)/2))) and (2−i(√5))^n =3^n e^(−inarctan(((√5)/2))) ⇒ A_n =3^n { e^(inarctan(((√5)/2))) +e^(−inarctan(((√5)/2))) } =3^n (2cos(n arctan(((√5)/2)))) =2.3^n cos(n arctan(((√5)/2))) also B_n =3^n { e^(inarctan(((√5)/2))) −e^(−inarctan(((√5)/2))) } =2i 3^n sin(narctan(((√5)/2)))
$${we}\:{have}\:\mid\mathrm{2}+{i}\sqrt{\mathrm{5}}\mid\:=\sqrt{\mathrm{2}^{\mathrm{2}} \:+\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{4}+\mathrm{5}}=\mathrm{3}\:\Rightarrow \\ $$$$\mathrm{2}+{i}\sqrt{\mathrm{5}}=\mathrm{3}\left(\frac{\mathrm{2}}{\mathrm{3}}\:+{i}\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\right)\:=\mathrm{3}\:{e}^{{iarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \:\Rightarrow\left(\mathrm{2}+{i}\sqrt{\mathrm{5}}\right)^{{n}} \:=\mathrm{3}^{{n}} \:{e}^{{inarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \\ $$$${and}\:\left(\mathrm{2}−{i}\sqrt{\mathrm{5}}\right)^{{n}} \:=\mathrm{3}^{{n}} \:{e}^{−{inarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \:\Rightarrow \\ $$$${A}_{{n}} =\mathrm{3}^{{n}} \left\{\:{e}^{{inarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \:+{e}^{−{inarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \right\}\:=\mathrm{3}^{{n}} \left(\mathrm{2}{cos}\left({n}\:{arctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right)\right) \\ $$$$=\mathrm{2}.\mathrm{3}^{{n}} \:{cos}\left({n}\:{arctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right)\:\:{also}\: \\ $$$${B}_{{n}} =\mathrm{3}^{{n}} \left\{\:{e}^{{inarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} −{e}^{−{inarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} \right\} \\ $$$$=\mathrm{2}{i}\:\mathrm{3}^{{n}} \:{sin}\left({narctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right) \\ $$
Answered by mr W last updated on 06/Aug/19
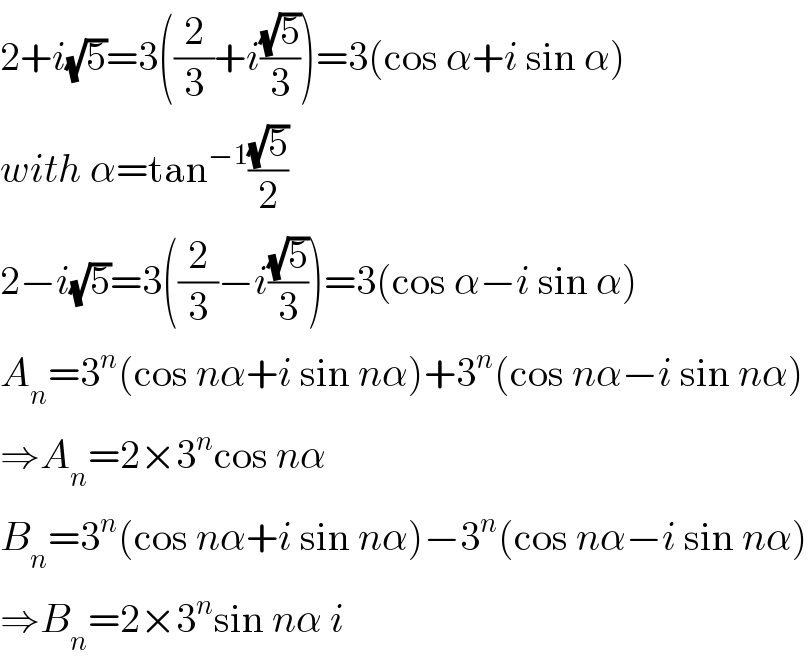
2+i(√5)=3((2/3)+i((√5)/3))=3(cos α+i sin α) with α=tan^(−1) ((√5)/2) 2−i(√5)=3((2/3)−i((√5)/3))=3(cos α−i sin α) A_n =3^n (cos nα+i sin nα)+3^n (cos nα−i sin nα) ⇒A_n =2×3^n cos nα B_n =3^n (cos nα+i sin nα)−3^n (cos nα−i sin nα) ⇒B_n =2×3^n sin nα i
$$\mathrm{2}+{i}\sqrt{\mathrm{5}}=\mathrm{3}\left(\frac{\mathrm{2}}{\mathrm{3}}+{i}\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\right)=\mathrm{3}\left(\mathrm{cos}\:\alpha+{i}\:\mathrm{sin}\:\alpha\right) \\ $$$${with}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{2}−{i}\sqrt{\mathrm{5}}=\mathrm{3}\left(\frac{\mathrm{2}}{\mathrm{3}}−{i}\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}\right)=\mathrm{3}\left(\mathrm{cos}\:\alpha−{i}\:\mathrm{sin}\:\alpha\right) \\ $$$${A}_{{n}} =\mathrm{3}^{{n}} \left(\mathrm{cos}\:{n}\alpha+{i}\:\mathrm{sin}\:{n}\alpha\right)+\mathrm{3}^{{n}} \left(\mathrm{cos}\:{n}\alpha−{i}\:\mathrm{sin}\:{n}\alpha\right) \\ $$$$\Rightarrow{A}_{{n}} =\mathrm{2}×\mathrm{3}^{{n}} \mathrm{cos}\:{n}\alpha \\ $$$${B}_{{n}} =\mathrm{3}^{{n}} \left(\mathrm{cos}\:{n}\alpha+{i}\:\mathrm{sin}\:{n}\alpha\right)−\mathrm{3}^{{n}} \left(\mathrm{cos}\:{n}\alpha−{i}\:\mathrm{sin}\:{n}\alpha\right) \\ $$$$\Rightarrow{B}_{{n}} =\mathrm{2}×\mathrm{3}^{{n}} \mathrm{sin}\:{n}\alpha\:{i} \\ $$

Pin