Menu Close

simplify-p-2-2pq-q-2-p-3-pq-2-p-2-q-q-3-

Tinku Tara 0 Comments
Pin




Question Number 66855 by John Kaloki Musau last updated on 20/Aug/19
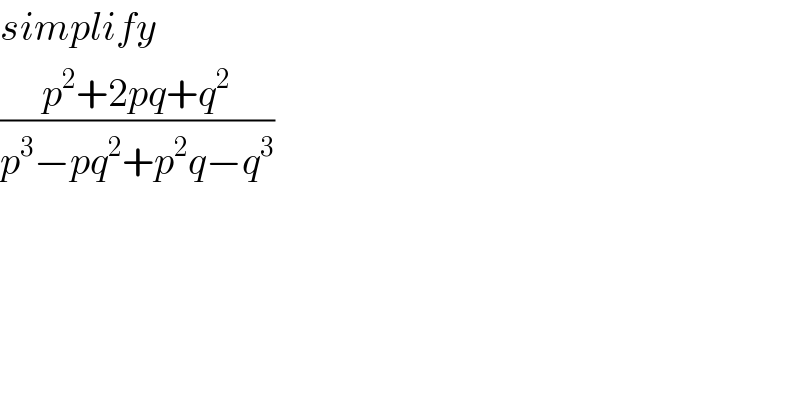
simplify ((p^2 +2pq+q^2 )/(p^3 −pq^2 +p^2 q−q^3 ))
simplifyp2+2pq+q2p3−pq2+p2q−q3
Answered by $@ty@m123 last updated on 20/Aug/19
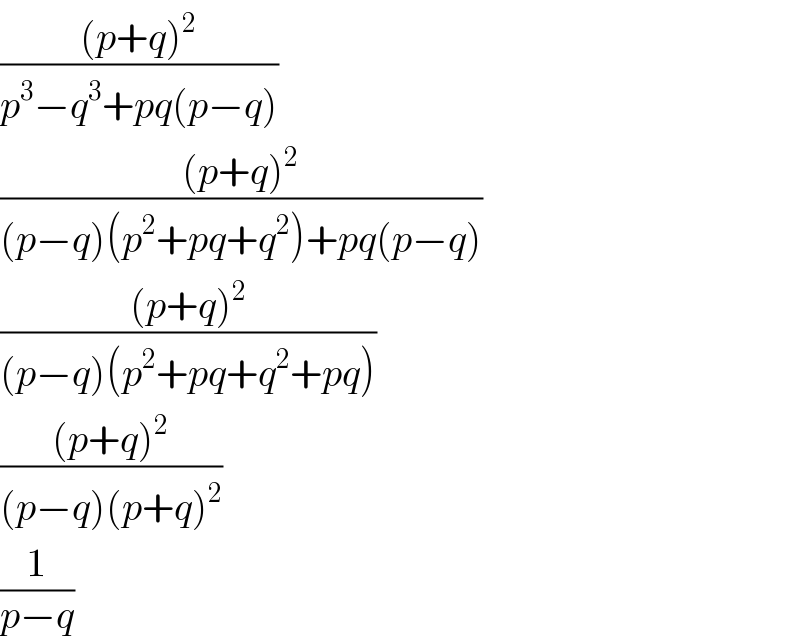
(((p+q)^2 )/(p^3 −q^3 +pq(p−q))) (((p+q)^2 )/((p−q)(p^2 +pq+q^2 )+pq(p−q))) (((p+q)^2 )/((p−q)(p^2 +pq+q^2 +pq))) (((p+q)^2 )/((p−q)(p+q)^2 )) (1/(p−q))
(p+q)2p3−q3+pq(p−q)(p+q)2(p−q)(p2+pq+q2)+pq(p−q)(p+q)2(p−q)(p2+pq+q2+pq)(p+q)2(p−q)(p+q)21p−q
Commented by John Kaloki Musau last updated on 20/Aug/19
wow! u got it.thanks
wow!ugotit.thanks
Answered by Mr Jor last updated on 25/Aug/19
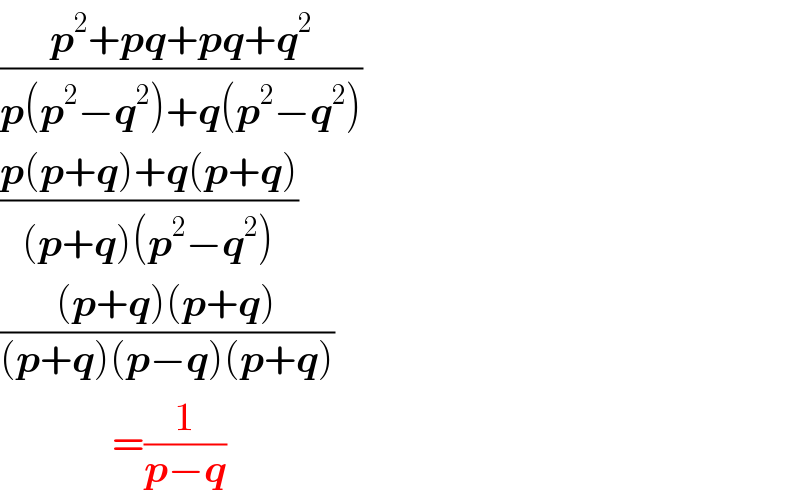
((p^2 +pq+pq+q^2 )/(p(p^2 −q^2 )+q(p^2 −q^2 ))) ((p(p+q)+q(p+q))/((p+q)(p^2 −q^2 ))) (((p+q)(p+q))/((p+q)(p−q)(p+q))) =(1/(p−q))
p2+pq+pq+q2p(p2−q2)+q(p2−q2)p(p+q)+q(p+q)(p+q)(p2−q2)(p+q)(p+q)(p+q)(p−q)(p+q)=1p−q

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *