Question Number 7959 by tawakalitu last updated on 25/Sep/16
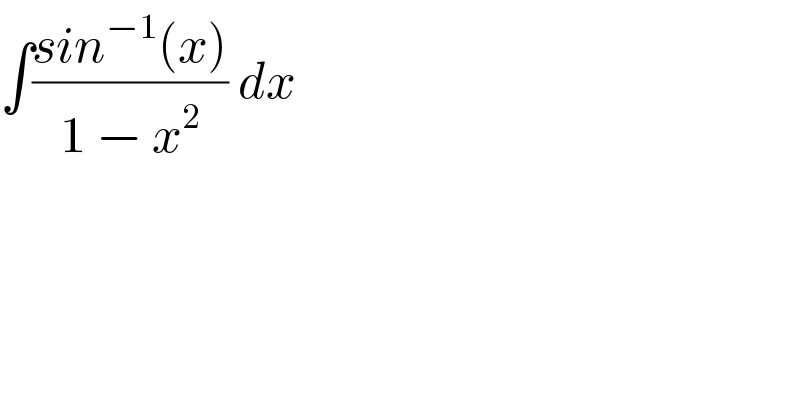
$$\int\frac{{sin}^{−\mathrm{1}} \left({x}\right)}{\mathrm{1}\:−\:{x}^{\mathrm{2}} }\:{dx} \\ $$
Commented by nick last updated on 26/Sep/16
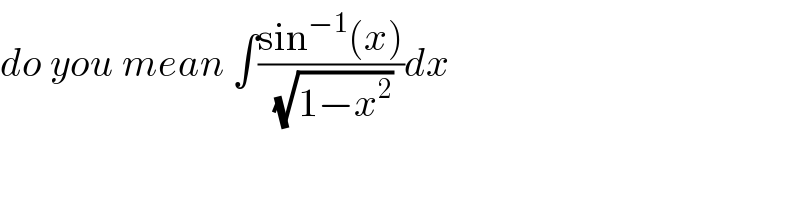
$${do}\:{you}\:{mean}\:\int\frac{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$
Commented by tawakalitu last updated on 26/Sep/16
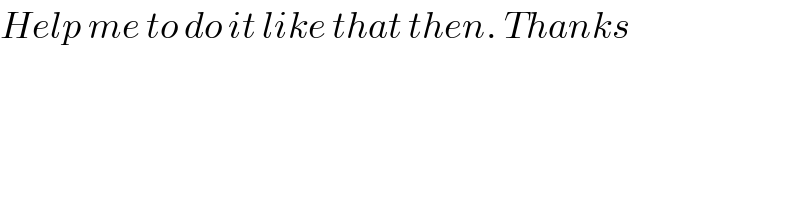
$${Help}\:{me}\:{to}\:{do}\:{it}\:{like}\:{that}\:{then}.\:{Thanks} \\ $$
Answered by nick last updated on 26/Sep/16
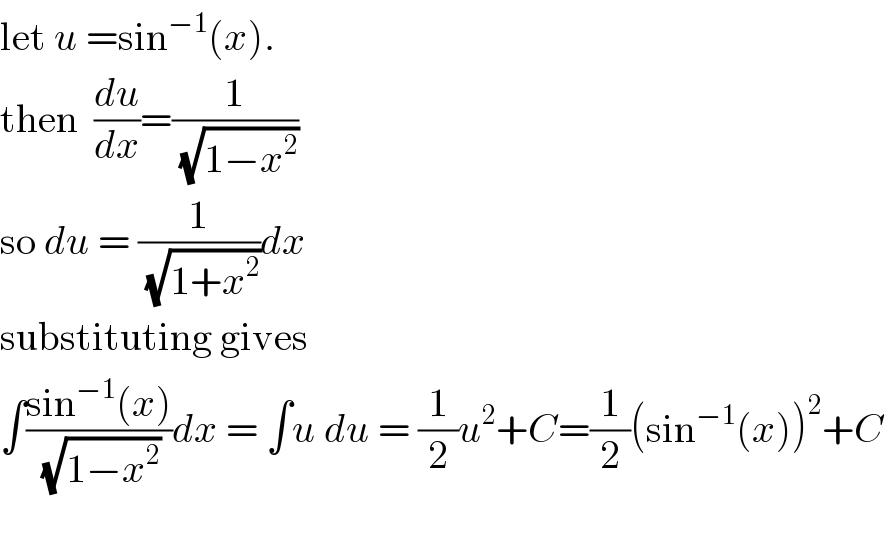
$$\mathrm{let}\:{u}\:=\mathrm{sin}^{−\mathrm{1}} \left({x}\right). \\ $$$$\mathrm{then}\:\:\frac{{du}}{{dx}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{so}\:{du}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{dx} \\ $$$$\mathrm{substituting}\:\mathrm{gives} \\ $$$$\int\frac{\mathrm{sin}^{−\mathrm{1}} \left({x}\right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\:=\:\int{u}\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{u}^{\mathrm{2}} +{C}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} +{C} \\ $$$$ \\ $$
Commented by tawakalitu last updated on 26/Sep/16
$${Thanks}\:{so}\:{much}.\:{i}\:{really}\:{appreciate}. \\ $$
