Menu Close

sin-101x-sin-90-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 7385 by Tawakalitu. last updated on 25/Aug/16
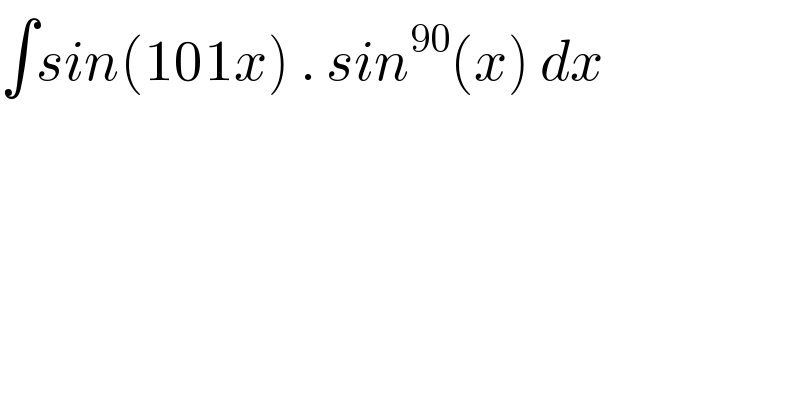
∫sin(101x) . sin^(90) (x) dx
$$\int{sin}\left(\mathrm{101}{x}\right)\:.\:{sin}^{\mathrm{90}} \left({x}\right)\:{dx} \\ $$
Commented by Yozzia last updated on 26/Aug/16
Let I(n)=∫e^(101ix) sin^n xdx (n∈Z^≥ i=(√(−1))) I(n)=∫e^(101ix) sin^2 xsin^(n−2) xdx I(n)=∫e^(101xi) (1−cos^2 x)sin^(n−2) xdx I(n)=I(n−2)−∫e^(101ix) cosx{cosxsin^(n−2) x}dx I(n)=I(n−2)−[e^(101ix) cosx(1/(n−1))sin^(n−1) x−(1/(n−1))∫sin^(n−1) xe^(101ix) {101icosx−sinx}dx I(n)−I(n−2)=((101i)/(n−1))∫e^(101ix) sin^(n−1) xcosxdx−(1/(n−1))∫e^(101ix) sin^n xdx−((e^(101ix) cosxsin^(n−1) x)/(n−1)) I(n)−I(n−2)=((101i)/(n−1))∫e^(101ix) sin^(n−1) xcosxdx−(1/(n−1))I(n)−((e^(101ix) cosxsin^(n−1) x)/(n−1)) −−−−−−−−−−−−−−−−−−−−−−−−−− ∫e^(101ix) sin^(n−1) xcosxdx=e^(101ix) (1/n)sin^n x−((101i)/n)∫e^(101ix) sin^n xdx ∫e^(101ix) sin^(n−1) xcosxdx=e^(101ix) (1/n)sin^n x−((101i)/n)I(n) −−−−−−−−−−−−−−−−−−−−−−−−−− I(n)−I(n−2)=((101i)/(n−1)){(1/n)e^(101ix) sin^n x−((101i)/n)I(n)}−(1/(n−1))I(n)−((e^(101ix) cosxsin^(n−1) x)/(n−1)) (1+(1/(n−1)))I(n)−I(n−2)=((10201)/(n(n−1)))I(n)+((101ie^(101ix) sin^n x)/(n(n−1)))−((e^(101ix) cosxsin^(n−1) x)/(n−1)) (1+(1/(n−1))−((10201)/(n(n−1))))I(n)−I(n−2)=((101ie^(101ix) sin^n x)/(n(n−1)))−((e^(101ix) cosxsin^(n−1) x)/(n−1)) ((n^2 −10201)/(n(n−1)))I(n)−I(n−2)=((101ie^(101ix) sin^n x)/(n(n−1)))−((e^(101ix) cosxsin^(n−1) x)/(n−1)) ⇒Im{((n^2 −10201)/(n(n−1)))I(n)−I(n−2)}=Im{((101ie^(101ix) sin^n x)/(n(n−1)))−((e^(101ix) cosxsin^(n−1) x)/(n−1))} −−−−−−−−−−−−−−−−−−−−−−−−−−−−− I(n)=∫e^(101ix) sin^n xdx=∫cos101xsin^n xdx+i∫sin101xsin^n xdx ⇒Im{I(n)}=Q(n)=∫sin101xsin^n xdx ∴Im{I(n−2)}=Q(n−2)=∫sin101xsin^(n−2) xdx −−−−−−−−−−−−−−−−−−−−−−−−−− Im{((101ie^(101ix) sin^n x)/(n(n−1)))−((e^(101ix) cosxsin^(n−1) x)/(n−1))} =((101cos101xsin^n x)/(n(n−1)))−((cosxsin101xsin^(n−1) x)/(n−1)) −−−−−−−−−−−−−−−−−−−−−−−−− ∴((n^2 −10201)/(n(n−1)))Q(n)−Q(n−2)=f(n,x) where f(n,x)=((101cos101xsin^n x)/(n(n−1)))−((cosxsin101xsin^(n−1) x)/(n−1)). ∴(n^2 −10201)Q(n)−n(n−1)Q(n−2)=n(n−1)f(n,x) (n≥2) (n−101)(n+101)Q(n)−n(n−1)Q(n−2)=n(n−1)f(n,x) Q(n)=g(n){Q(n−2)+f(n,x)} where g(n)=((n(n−1))/(n^2 −10201)) (n≠101). For say n=8, Q(2)=g(2){Q(0)+f(2,x)} Q(4)=g(4){Q(2)+f(4,x)} =g(4)g(2){Q(0)+f(2,x)}+g(4)f(4,x) Q(4)=g(4)g(2)Q(0)+g(4)g(2)f(2,x)+g(4)f(4,x) Q(6)=g(6){Q(4)+f(6,x)} =g(6)g(4)g(2){Q(0)+f(2,x)}+g(6)g(4)f(4,x)+g(6)f(6,x) Q(8)=g(8){Q(6)+f(8,x)} ={Π_(i=1) ^4 g(2i)}{Q(0)+f(2,x)}+(1/(g(2))){Π_(i=1) ^4 g(2i)}f(4,x)+(1/(g(2)g(4))){Π_(i=1) ^4 g(2i)}f(6,x)+(1/(g(2)g(4)g(6))){Π_(i=1) ^4 g(2i)}f(8,x)
$${Let}\:{I}\left({n}\right)=\int{e}^{\mathrm{101}{ix}} {sin}^{{n}} {xdx}\:\:\:\left({n}\in\mathbb{Z}^{\geqslant} \:{i}=\sqrt{−\mathrm{1}}\right) \\ $$$${I}\left({n}\right)=\int{e}^{\mathrm{101}{ix}} {sin}^{\mathrm{2}} {xsin}^{{n}−\mathrm{2}} {xdx} \\ $$$${I}\left({n}\right)=\int{e}^{\mathrm{101}{xi}} \left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){sin}^{{n}−\mathrm{2}} {xdx} \\ $$$${I}\left({n}\right)={I}\left({n}−\mathrm{2}\right)−\int{e}^{\mathrm{101}{ix}} {cosx}\left\{{cosxsin}^{{n}−\mathrm{2}} {x}\right\}{dx} \\ $$$${I}\left({n}\right)={I}\left({n}−\mathrm{2}\right)−\left[{e}^{\mathrm{101}{ix}} {cosx}\frac{\mathrm{1}}{{n}−\mathrm{1}}{sin}^{{n}−\mathrm{1}} {x}−\frac{\mathrm{1}}{{n}−\mathrm{1}}\int{sin}^{{n}−\mathrm{1}} {xe}^{\mathrm{101}{ix}} \left\{\mathrm{101}{icosx}−{sinx}\right\}{dx}\right. \\ $$$${I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)=\frac{\mathrm{101}{i}}{{n}−\mathrm{1}}\int{e}^{\mathrm{101}{ix}} {sin}^{{n}−\mathrm{1}} {xcosxdx}−\frac{\mathrm{1}}{{n}−\mathrm{1}}\int{e}^{\mathrm{101}{ix}} {sin}^{{n}} {xdx}−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$${I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)=\frac{\mathrm{101}{i}}{{n}−\mathrm{1}}\int{e}^{\mathrm{101}{ix}} {sin}^{{n}−\mathrm{1}} {xcosxdx}−\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}\left({n}\right)−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\int{e}^{\mathrm{101}{ix}} {sin}^{{n}−\mathrm{1}} {xcosxdx}={e}^{\mathrm{101}{ix}} \frac{\mathrm{1}}{{n}}{sin}^{{n}} {x}−\frac{\mathrm{101}{i}}{{n}}\int{e}^{\mathrm{101}{ix}} {sin}^{{n}} {xdx} \\ $$$$\int{e}^{\mathrm{101}{ix}} {sin}^{{n}−\mathrm{1}} {xcosxdx}={e}^{\mathrm{101}{ix}} \frac{\mathrm{1}}{{n}}{sin}^{{n}} {x}−\frac{\mathrm{101}{i}}{{n}}{I}\left({n}\right) \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)=\frac{\mathrm{101}{i}}{{n}−\mathrm{1}}\left\{\frac{\mathrm{1}}{{n}}{e}^{\mathrm{101}{ix}} {sin}^{{n}} {x}−\frac{\mathrm{101}{i}}{{n}}{I}\left({n}\right)\right\}−\frac{\mathrm{1}}{{n}−\mathrm{1}}{I}\left({n}\right)−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}−\mathrm{1}}\right){I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)=\frac{\mathrm{10201}}{{n}\left({n}−\mathrm{1}\right)}{I}\left({n}\right)+\frac{\mathrm{101}{ie}^{\mathrm{101}{ix}} {sin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{10201}}{{n}\left({n}−\mathrm{1}\right)}\right){I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)=\frac{\mathrm{101}{ie}^{\mathrm{101}{ix}} {sin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$$\frac{{n}^{\mathrm{2}} −\mathrm{10201}}{{n}\left({n}−\mathrm{1}\right)}{I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)=\frac{\mathrm{101}{ie}^{\mathrm{101}{ix}} {sin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$$\Rightarrow{Im}\left\{\frac{{n}^{\mathrm{2}} −\mathrm{10201}}{{n}\left({n}−\mathrm{1}\right)}{I}\left({n}\right)−{I}\left({n}−\mathrm{2}\right)\right\}={Im}\left\{\frac{\mathrm{101}{ie}^{\mathrm{101}{ix}} {sin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}}\right\} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${I}\left({n}\right)=\int{e}^{\mathrm{101}{ix}} {sin}^{{n}} {xdx}=\int{cos}\mathrm{101}{xsin}^{{n}} {xdx}+{i}\int{sin}\mathrm{101}{xsin}^{{n}} {xdx} \\ $$$$\Rightarrow{Im}\left\{{I}\left({n}\right)\right\}={Q}\left({n}\right)=\int{sin}\mathrm{101}{xsin}^{{n}} {xdx} \\ $$$$\therefore{Im}\left\{{I}\left({n}−\mathrm{2}\right)\right\}={Q}\left({n}−\mathrm{2}\right)=\int{sin}\mathrm{101}{xsin}^{{n}−\mathrm{2}} {xdx} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Im}\left\{\frac{\mathrm{101}{ie}^{\mathrm{101}{ix}} {sin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{e}^{\mathrm{101}{ix}} {cosxsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{101}{cos}\mathrm{101}{xsin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{cosxsin}\mathrm{101}{xsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\therefore\frac{{n}^{\mathrm{2}} −\mathrm{10201}}{{n}\left({n}−\mathrm{1}\right)}{Q}\left({n}\right)−{Q}\left({n}−\mathrm{2}\right)={f}\left({n},{x}\right) \\ $$$${where}\:{f}\left({n},{x}\right)=\frac{\mathrm{101}{cos}\mathrm{101}{xsin}^{{n}} {x}}{{n}\left({n}−\mathrm{1}\right)}−\frac{{cosxsin}\mathrm{101}{xsin}^{{n}−\mathrm{1}} {x}}{{n}−\mathrm{1}}. \\ $$$$\therefore\left({n}^{\mathrm{2}} −\mathrm{10201}\right){Q}\left({n}\right)−{n}\left({n}−\mathrm{1}\right){Q}\left({n}−\mathrm{2}\right)={n}\left({n}−\mathrm{1}\right){f}\left({n},{x}\right)\:\:\left({n}\geqslant\mathrm{2}\right) \\ $$$$\left({n}−\mathrm{101}\right)\left({n}+\mathrm{101}\right){Q}\left({n}\right)−{n}\left({n}−\mathrm{1}\right){Q}\left({n}−\mathrm{2}\right)={n}\left({n}−\mathrm{1}\right){f}\left({n},{x}\right) \\ $$$${Q}\left({n}\right)={g}\left({n}\right)\left\{{Q}\left({n}−\mathrm{2}\right)+{f}\left({n},{x}\right)\right\}\:\: \\ $$$${where}\:{g}\left({n}\right)=\frac{{n}\left({n}−\mathrm{1}\right)}{{n}^{\mathrm{2}} −\mathrm{10201}}\:\:\:\left({n}\neq\mathrm{101}\right). \\ $$$${For}\:{say}\:{n}=\mathrm{8}, \\ $$$${Q}\left(\mathrm{2}\right)={g}\left(\mathrm{2}\right)\left\{{Q}\left(\mathrm{0}\right)+{f}\left(\mathrm{2},{x}\right)\right\} \\ $$$${Q}\left(\mathrm{4}\right)={g}\left(\mathrm{4}\right)\left\{{Q}\left(\mathrm{2}\right)+{f}\left(\mathrm{4},{x}\right)\right\} \\ $$$$={g}\left(\mathrm{4}\right){g}\left(\mathrm{2}\right)\left\{{Q}\left(\mathrm{0}\right)+{f}\left(\mathrm{2},{x}\right)\right\}+{g}\left(\mathrm{4}\right){f}\left(\mathrm{4},{x}\right) \\ $$$${Q}\left(\mathrm{4}\right)={g}\left(\mathrm{4}\right){g}\left(\mathrm{2}\right){Q}\left(\mathrm{0}\right)+{g}\left(\mathrm{4}\right){g}\left(\mathrm{2}\right){f}\left(\mathrm{2},{x}\right)+{g}\left(\mathrm{4}\right){f}\left(\mathrm{4},{x}\right) \\ $$$${Q}\left(\mathrm{6}\right)={g}\left(\mathrm{6}\right)\left\{{Q}\left(\mathrm{4}\right)+{f}\left(\mathrm{6},{x}\right)\right\} \\ $$$$={g}\left(\mathrm{6}\right){g}\left(\mathrm{4}\right){g}\left(\mathrm{2}\right)\left\{{Q}\left(\mathrm{0}\right)+{f}\left(\mathrm{2},{x}\right)\right\}+{g}\left(\mathrm{6}\right){g}\left(\mathrm{4}\right){f}\left(\mathrm{4},{x}\right)+{g}\left(\mathrm{6}\right){f}\left(\mathrm{6},{x}\right) \\ $$$${Q}\left(\mathrm{8}\right)={g}\left(\mathrm{8}\right)\left\{{Q}\left(\mathrm{6}\right)+{f}\left(\mathrm{8},{x}\right)\right\} \\ $$$$=\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{g}\left(\mathrm{2}{i}\right)\right\}\left\{{Q}\left(\mathrm{0}\right)+{f}\left(\mathrm{2},{x}\right)\right\}+\frac{\mathrm{1}}{{g}\left(\mathrm{2}\right)}\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{g}\left(\mathrm{2}{i}\right)\right\}{f}\left(\mathrm{4},{x}\right)+\frac{\mathrm{1}}{{g}\left(\mathrm{2}\right){g}\left(\mathrm{4}\right)}\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{g}\left(\mathrm{2}{i}\right)\right\}{f}\left(\mathrm{6},{x}\right)+\frac{\mathrm{1}}{{g}\left(\mathrm{2}\right){g}\left(\mathrm{4}\right){g}\left(\mathrm{6}\right)}\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{g}\left(\mathrm{2}{i}\right)\right\}{f}\left(\mathrm{8},{x}\right)\:\: \\ $$
Commented by Tawakalitu. last updated on 25/Aug/16
Wow , thank you sir. God bless you.
$${Wow}\:,\:{thank}\:{you}\:{sir}.\:{God}\:{bless}\:{you}. \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 26/Aug/16
I really appreciate sir.
$${I}\:{really}\:{appreciate}\:{sir}. \\ $$
Commented by Tawakalitu. last updated on 26/Aug/16
I really appreciate sir.
$${I}\:{really}\:{appreciate}\:{sir}. \\ $$
Commented by Yozzia last updated on 26/Aug/16
Q(8)={Π_(i=1) ^4 g(2i)}{Q(0)+f(2,x)+(1/(g(2)))f(4,x)+(1/(g(2)g(4)))f(6,x)+(1/(g(2)g(4)g(6)))f(8,x)} ∴ For n=90, Q(90)={Π_(i=1) ^(45) g(2i)}{Q(0)+f(2,x)+Σ_(k=2) ^(45) ((f(2k,x))/(Π_(i=1) ^(k−1) g(2i)))} Q(0)=∫sin101xsin^0 xdx=((−1)/(101))cos101x+c ∴ Q(90)={Π_(i=1) ^(45) ((2i(2i−1))/(4i^2 −10201))}{((101cos101xsin^2 x)/2)−((sin2x)/2)sin101x−((cosx)/(101))+Σ_(k=2) ^(45) [((((101cos101xsin^(2i) x)/(2i(2i−1)))−((cosxsin101xsin^(2i−1) x)/(2i−1)))/(Π_(i=1) ^(k−1) ((2i(2i−1))/(4i^2 −10201))))]}+D ∫sin(101x)sin^(90) xdx={Π_(i=1) ^(45) ((2i(2i−1))/(4i^2 −10201))}{((101cos101xsin^2 x)/2)−((sin2x)/2)sin101x−((cosx)/(101))+Σ_(k=2) ^(45) [((((101cos101xsin^(2i) x)/(2i(2i−1)))−((cosxsin101xsin^(2i−1) x)/(2i−1)))/(Π_(i=1) ^(k−1) ((2i(2i−1))/(4i^2 −10201))))]}+D
$${Q}\left(\mathrm{8}\right)=\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\prod}}{g}\left(\mathrm{2}{i}\right)\right\}\left\{{Q}\left(\mathrm{0}\right)+{f}\left(\mathrm{2},{x}\right)+\frac{\mathrm{1}}{{g}\left(\mathrm{2}\right)}{f}\left(\mathrm{4},{x}\right)+\frac{\mathrm{1}}{{g}\left(\mathrm{2}\right){g}\left(\mathrm{4}\right)}{f}\left(\mathrm{6},{x}\right)+\frac{\mathrm{1}}{{g}\left(\mathrm{2}\right){g}\left(\mathrm{4}\right){g}\left(\mathrm{6}\right)}{f}\left(\mathrm{8},{x}\right)\right\} \\ $$$$ \\ $$$$\therefore\:{For}\:{n}=\mathrm{90}, \\ $$$${Q}\left(\mathrm{90}\right)=\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}{g}\left(\mathrm{2}{i}\right)\right\}\left\{{Q}\left(\mathrm{0}\right)+{f}\left(\mathrm{2},{x}\right)+\underset{{k}=\mathrm{2}} {\overset{\mathrm{45}} {\sum}}\frac{{f}\left(\mathrm{2}{k},{x}\right)}{\underset{{i}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\prod}}{g}\left(\mathrm{2}{i}\right)}\right\} \\ $$$${Q}\left(\mathrm{0}\right)=\int{sin}\mathrm{101}{xsin}^{\mathrm{0}} {xdx}=\frac{−\mathrm{1}}{\mathrm{101}}{cos}\mathrm{101}{x}+{c} \\ $$$$\therefore\:{Q}\left(\mathrm{90}\right)=\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\frac{\mathrm{2}{i}\left(\mathrm{2}{i}−\mathrm{1}\right)}{\mathrm{4}{i}^{\mathrm{2}} −\mathrm{10201}}\right\}\left\{\frac{\mathrm{101}{cos}\mathrm{101}{xsin}^{\mathrm{2}} {x}}{\mathrm{2}}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}{sin}\mathrm{101}{x}−\frac{{cosx}}{\mathrm{101}}+\underset{{k}=\mathrm{2}} {\overset{\mathrm{45}} {\sum}}\left[\frac{\frac{\mathrm{101}{cos}\mathrm{101}{xsin}^{\mathrm{2}{i}} {x}}{\mathrm{2}{i}\left(\mathrm{2}{i}−\mathrm{1}\right)}−\frac{{cosxsin}\mathrm{101}{xsin}^{\mathrm{2}{i}−\mathrm{1}} {x}}{\mathrm{2}{i}−\mathrm{1}}}{\underset{{i}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\prod}}\frac{\mathrm{2}{i}\left(\mathrm{2}{i}−\mathrm{1}\right)}{\mathrm{4}{i}^{\mathrm{2}} −\mathrm{10201}}}\right]\right\}+{D} \\ $$$$\int{sin}\left(\mathrm{101}{x}\right){sin}^{\mathrm{90}} {xdx}=\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{45}} {\prod}}\frac{\mathrm{2}{i}\left(\mathrm{2}{i}−\mathrm{1}\right)}{\mathrm{4}{i}^{\mathrm{2}} −\mathrm{10201}}\right\}\left\{\frac{\mathrm{101}{cos}\mathrm{101}{xsin}^{\mathrm{2}} {x}}{\mathrm{2}}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}{sin}\mathrm{101}{x}−\frac{{cosx}}{\mathrm{101}}+\underset{{k}=\mathrm{2}} {\overset{\mathrm{45}} {\sum}}\left[\frac{\frac{\mathrm{101}{cos}\mathrm{101}{xsin}^{\mathrm{2}{i}} {x}}{\mathrm{2}{i}\left(\mathrm{2}{i}−\mathrm{1}\right)}−\frac{{cosxsin}\mathrm{101}{xsin}^{\mathrm{2}{i}−\mathrm{1}} {x}}{\mathrm{2}{i}−\mathrm{1}}}{\underset{{i}=\mathrm{1}} {\overset{{k}−\mathrm{1}} {\prod}}\frac{\mathrm{2}{i}\left(\mathrm{2}{i}−\mathrm{1}\right)}{\mathrm{4}{i}^{\mathrm{2}} −\mathrm{10201}}}\right]\right\}+{D} \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 26/Aug/16
I really appreciate sir. God bless you
$${I}\:{really}\:{appreciate}\:{sir}. \\ $$$${God}\:{bless}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *