Question Number 70719 by oyemi kemewari last updated on 07/Oct/19
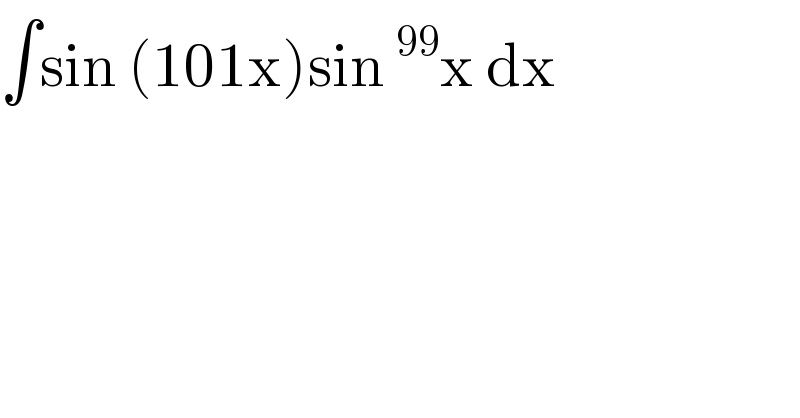
$$\int\mathrm{sin}\:\left(\mathrm{101x}\right)\mathrm{sin}\:^{\mathrm{99}} \mathrm{x}\:\mathrm{dx} \\ $$
Answered by mind is power last updated on 07/Oct/19
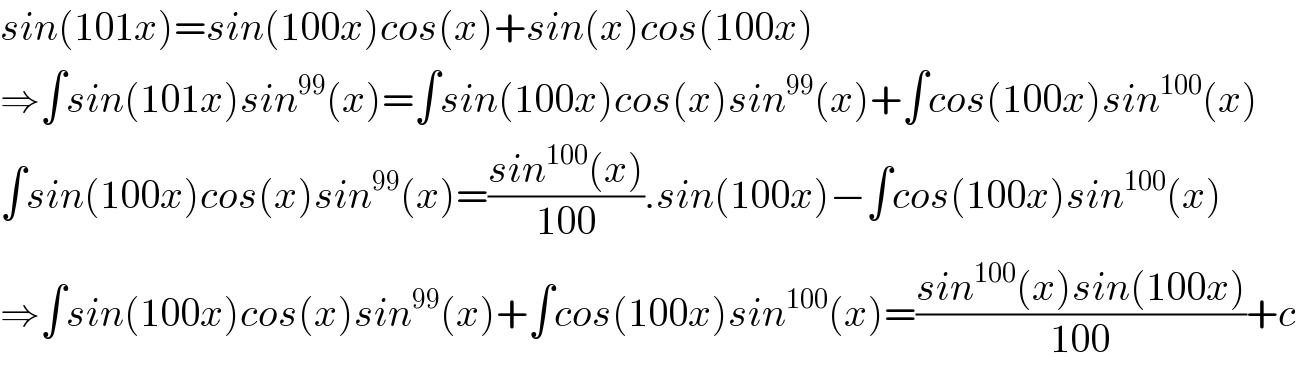
$${sin}\left(\mathrm{101}{x}\right)={sin}\left(\mathrm{100}{x}\right){cos}\left({x}\right)+{sin}\left({x}\right){cos}\left(\mathrm{100}{x}\right) \\ $$$$\Rightarrow\int{sin}\left(\mathrm{101}{x}\right){sin}^{\mathrm{99}} \left({x}\right)=\int{sin}\left(\mathrm{100}{x}\right){cos}\left({x}\right){sin}^{\mathrm{99}} \left({x}\right)+\int{cos}\left(\mathrm{100}{x}\right){sin}^{\mathrm{100}} \left({x}\right) \\ $$$$\int{sin}\left(\mathrm{100}{x}\right){cos}\left({x}\right){sin}^{\mathrm{99}} \left({x}\right)=\frac{{sin}^{\mathrm{100}} \left({x}\right)}{\mathrm{100}}.{sin}\left(\mathrm{100}{x}\right)−\int{cos}\left(\mathrm{100}{x}\right){sin}^{\mathrm{100}} \left({x}\right) \\ $$$$\Rightarrow\int{sin}\left(\mathrm{100}{x}\right){cos}\left({x}\right){sin}^{\mathrm{99}} \left({x}\right)+\int{cos}\left(\mathrm{100}{x}\right){sin}^{\mathrm{100}} \left({x}\right)=\frac{{sin}^{\mathrm{100}} \left({x}\right){sin}\left(\mathrm{100}{x}\right)}{\mathrm{100}}+{c} \\ $$
