Question Number 71146 by sadimuhmud 136 last updated on 12/Oct/19
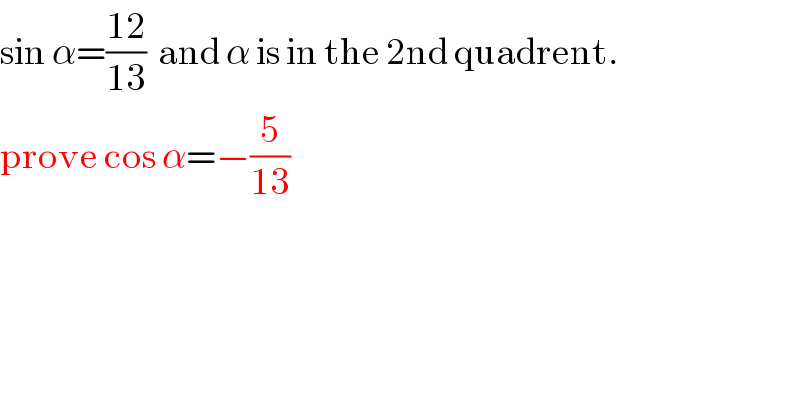
$$\mathrm{sin}\:\alpha=\frac{\mathrm{12}}{\mathrm{13}}\:\:\mathrm{and}\:\alpha\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{2nd}\:\mathrm{quadrent}. \\ $$$$\mathrm{prove}\:\mathrm{cos}\:\alpha=−\frac{\mathrm{5}}{\mathrm{13}} \\ $$
Commented by Rio Michael last updated on 12/Oct/19
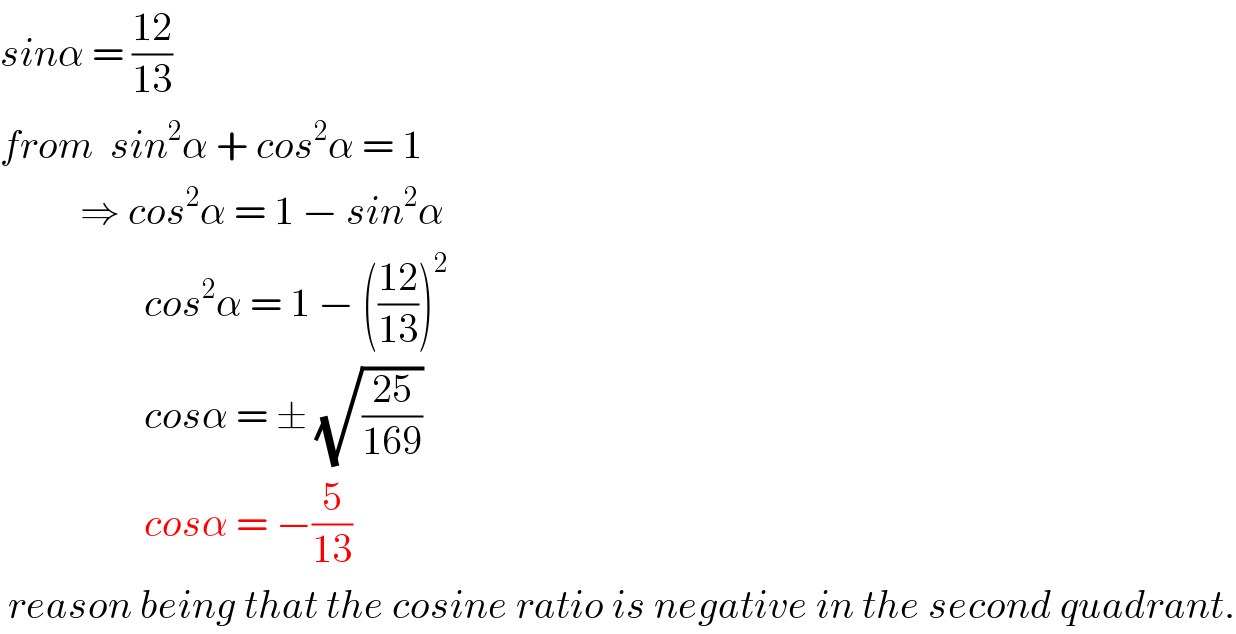
$${sin}\alpha\:=\:\frac{\mathrm{12}}{\mathrm{13}} \\ $$$${from}\:\:{sin}^{\mathrm{2}} \alpha\:+\:{cos}^{\mathrm{2}} \alpha\:=\:\mathrm{1}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{cos}^{\mathrm{2}} \alpha\:=\:\mathrm{1}\:−\:{sin}^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cos}^{\mathrm{2}} \alpha\:=\:\mathrm{1}\:−\:\left(\frac{\mathrm{12}}{\mathrm{13}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cos}\alpha\:=\:\pm\:\sqrt{\frac{\mathrm{25}}{\mathrm{169}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{cos}\alpha\:=\:−\frac{\mathrm{5}}{\mathrm{13}} \\ $$$$\:{reason}\:{being}\:{that}\:{the}\:{cosine}\:{ratio}\:{is}\:{negative}\:{in}\:{the}\:{second}\:{quadrant}. \\ $$
Answered by Kunal12588 last updated on 12/Oct/19
![sin α = ((12)/(13)) using identity :− sin^2 θ + cos^2 θ=1 ⇒cos α = −((√(13^2 −12^2 ))/(13)) [∵ (π/2)<α≤π] ⇒cos α = −((√(169−144))/(13))=−((√(25))/(13))=−(5/(13))](https://www.tinkutara.com/question/Q71166.png)
$${sin}\:\alpha\:=\:\frac{\mathrm{12}}{\mathrm{13}} \\ $$$${using}\:{identity}\::−\:\mathrm{sin}^{\mathrm{2}} \:\theta\:+\:\mathrm{cos}^{\mathrm{2}} \:\theta=\mathrm{1}\:\: \\ $$$$\Rightarrow{cos}\:\alpha\:=\:−\frac{\sqrt{\mathrm{13}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} }}{\mathrm{13}}\:\:\left[\because\:\frac{\pi}{\mathrm{2}}<\alpha\leqslant\pi\right] \\ $$$$\Rightarrow{cos}\:\alpha\:=\:−\frac{\sqrt{\mathrm{169}−\mathrm{144}}}{\mathrm{13}}=−\frac{\sqrt{\mathrm{25}}}{\mathrm{13}}=−\frac{\mathrm{5}}{\mathrm{13}}\:\: \\ $$
