Question Number 12464 by tawa last updated on 23/Apr/17
$$\int\:\mathrm{sin}^{\mathrm{3}} \left(\mathrm{7x}\right)\:\mathrm{dx} \\ $$
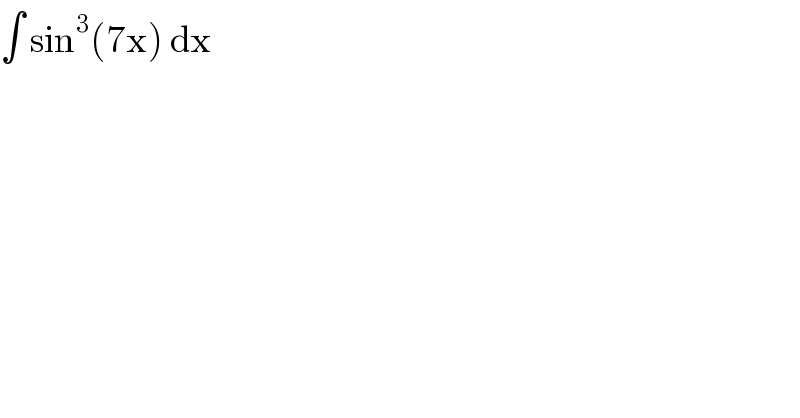
Answered by ajfour last updated on 23/Apr/17
![sin 3x=3sin x−4sin^3 x I=∫sin^3 (7x)dx =(1/4)∫[3sin (7x)−sin 3(7x)]dx =(1/4)(−(3/7)cos (7x)+((cos (21x))/(21)) )+C =−((3cos (7x))/(28))+((cos (21x))/(84))+C](https://www.tinkutara.com/question/Q12469.png)
$$\mathrm{sin}\:\mathrm{3}{x}=\mathrm{3sin}\:{x}−\mathrm{4sin}\:^{\mathrm{3}} {x} \\ $$$${I}=\int\mathrm{sin}\:^{\mathrm{3}} \left(\mathrm{7}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int\left[\mathrm{3sin}\:\left(\mathrm{7}{x}\right)−\mathrm{sin}\:\mathrm{3}\left(\mathrm{7}{x}\right)\right]{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{3}}{\mathrm{7}}\mathrm{cos}\:\left(\mathrm{7}{x}\right)+\frac{\mathrm{cos}\:\left(\mathrm{21}{x}\right)}{\mathrm{21}}\:\right)+{C} \\ $$$$=−\frac{\mathrm{3cos}\:\left(\mathrm{7}{x}\right)}{\mathrm{28}}+\frac{\mathrm{cos}\:\left(\mathrm{21}{x}\right)}{\mathrm{84}}+{C} \\ $$
Commented by tawa last updated on 23/Apr/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by sma3l2996 last updated on 23/Apr/17
$$=\int\left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{7}{x}\right)\right){sin}\left(\mathrm{7}{x}\right){dx} \\ $$$$=\int{sin}\left(\mathrm{7}{x}\right){dx}−\int{sin}\left(\mathrm{7}{x}\right){cos}^{\mathrm{2}} \left(\mathrm{7}{x}\right){dx} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{7}}{cos}\left(\mathrm{7}{x}\right)+\frac{\mathrm{1}}{\mathrm{7}}\int{cos}'\left(\mathrm{7}{x}\right){cos}^{\mathrm{2}} \left(\mathrm{7}{x}\right){dx}+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}×\mathrm{7}}{cos}^{\mathrm{3}} \left(\mathrm{7}{x}\right)−\frac{\mathrm{1}}{\mathrm{7}}{cos}\left(\mathrm{7}{x}\right) \\ $$$$=\frac{{cos}\left(\mathrm{7}{x}\right)}{\mathrm{7}}\left(\frac{\mathrm{1}}{\mathrm{3}}{cos}^{\mathrm{2}} \left(\mathrm{7}{x}\right)−\mathrm{1}\right) \\ $$
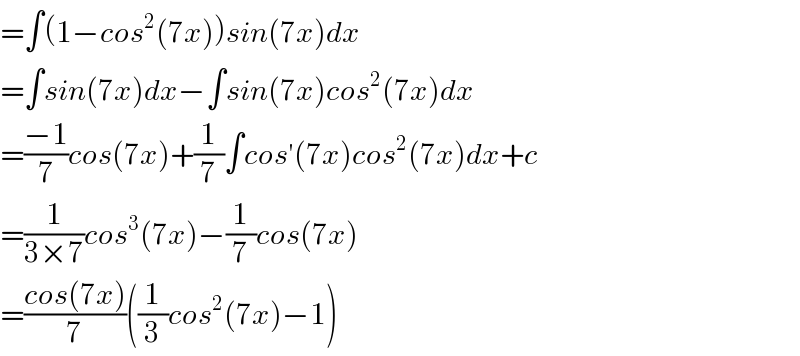
Commented by tawa last updated on 23/Apr/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mrW1 last updated on 23/Apr/17
![∫ sin^3 (7x) dx =(1/7)∫sin^3 (7x)d(7x) =(1/7)∫sin^3 t dt t=7x =−(1/7)∫sin^2 t d(cos t) =−(1/7)∫(1−cos^2 t) d(cos t) =−(1/7)∫(1−u^2 ) du u=cos t=cos (7x) =−(1/7)(∫du−∫u^2 du) =−(1/7)(u−(u^3 /3))+C =(u/(21))(u^2 −3)+C =((cos (7x))/(21))[cos^2 (7x)−3]+C](https://www.tinkutara.com/question/Q12477.png)
$$\int\:\mathrm{sin}^{\mathrm{3}} \left(\mathrm{7x}\right)\:\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}\int\mathrm{sin}^{\mathrm{3}} \:\left(\mathrm{7}{x}\right){d}\left(\mathrm{7}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}\int\mathrm{sin}^{\mathrm{3}} \:{t}\:{dt}\:\:\:\:\:\:\:\:\:{t}=\mathrm{7}{x} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\int\mathrm{sin}^{\mathrm{2}} \:{t}\:{d}\left(\mathrm{cos}\:{t}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\int\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{t}\right)\:{d}\left(\mathrm{cos}\:{t}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\int\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\:{du}\:\:\:\:\:\:\:\:\:{u}=\mathrm{cos}\:{t}=\mathrm{cos}\:\left(\mathrm{7}{x}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\left(\int{du}−\int{u}^{\mathrm{2}} {du}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\left({u}−\frac{{u}^{\mathrm{3}} }{\mathrm{3}}\right)+{C} \\ $$$$=\frac{{u}}{\mathrm{21}}\left({u}^{\mathrm{2}} −\mathrm{3}\right)+{C} \\ $$$$=\frac{\mathrm{cos}\:\left(\mathrm{7}{x}\right)}{\mathrm{21}}\left[\mathrm{cos}^{\mathrm{2}} \:\left(\mathrm{7}{x}\right)−\mathrm{3}\right]+{C} \\ $$
Commented by tawa last updated on 23/Apr/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$