Question Number 72153 by 20190927 last updated on 25/Oct/19
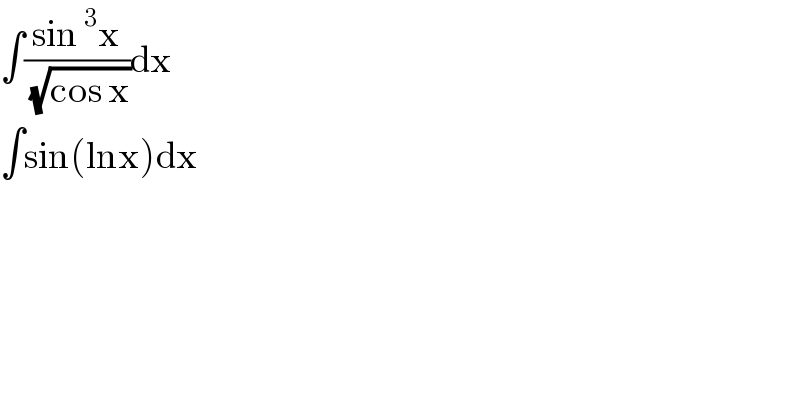
$$\int\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\:\sqrt{\mathrm{cos}\:\mathrm{x}}}\mathrm{dx} \\ $$$$\int\mathrm{sin}\left(\mathrm{lnx}\right)\mathrm{dx} \\ $$
Commented by Prithwish sen last updated on 25/Oct/19
![a) let cosx = t^2 ⇒−sinx dx= 2tdt −∫(((1−t^4 ).2tdt)/t) =− 2[∫dt−∫t^4 dt] =−2[t−(t^5 /5)] = 2[ (1/5) cos^(5/2) x−(√(cosx))] +C b) let x= e^t ⇒ dx = e^t dt ∫sint.e^t dt = I applying by parts I= e^t sint−∫e^t costdt = e^t .sint−{e^t cost+∫e^t sintdt} 2I=e^t (sint−cost) I = (1/2)x{sin(lnx)−cos(lnx)}+C please check.](https://www.tinkutara.com/question/Q72159.png)
$$\left.\boldsymbol{\mathrm{a}}\right)\:\mathrm{let}\:\mathrm{cosx}\:=\:\mathrm{t}^{\mathrm{2}} \Rightarrow−\mathrm{sinx}\:\mathrm{dx}=\:\mathrm{2tdt} \\ $$$$−\int\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{4}} \right).\mathrm{2tdt}}{\mathrm{t}}\:=−\:\mathrm{2}\left[\int\mathrm{dt}−\int\mathrm{t}^{\mathrm{4}} \mathrm{dt}\right] \\ $$$$=−\mathrm{2}\left[\mathrm{t}−\frac{\mathrm{t}^{\mathrm{5}} }{\mathrm{5}}\right]\:=\:\mathrm{2}\left[\:\frac{\mathrm{1}}{\mathrm{5}}\:\boldsymbol{\mathrm{cos}}^{\frac{\mathrm{5}}{\mathrm{2}}} \boldsymbol{\mathrm{x}}−\sqrt{\boldsymbol{\mathrm{cosx}}}\right]\:+\boldsymbol{\mathrm{C}} \\ $$$$\left.\boldsymbol{\mathrm{b}}\right)\:\:\mathrm{let}\:\mathrm{x}=\:\mathrm{e}^{\mathrm{t}} \:\Rightarrow\:\mathrm{dx}\:=\:\mathrm{e}^{\mathrm{t}} \mathrm{dt} \\ $$$$\int\mathrm{sint}.\mathrm{e}^{\mathrm{t}} \mathrm{dt}\:\:=\:\mathrm{I}\:\:\mathrm{applying}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{I}=\:\mathrm{e}^{\mathrm{t}} \mathrm{sint}−\int\mathrm{e}^{\mathrm{t}} \mathrm{costdt}\:=\:\mathrm{e}^{\mathrm{t}} .\mathrm{sint}−\left\{\mathrm{e}^{\mathrm{t}} \mathrm{cost}+\int\mathrm{e}^{\mathrm{t}} \mathrm{sintdt}\right\} \\ $$$$\mathrm{2I}=\mathrm{e}^{\mathrm{t}} \left(\mathrm{sint}−\mathrm{cost}\right) \\ $$$$\boldsymbol{\mathrm{I}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{x}}\left\{\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{lnx}}\right)−\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{lnx}}\right)\right\}+\boldsymbol{\mathrm{C}} \\ $$$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by 20190927 last updated on 25/Oct/19
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Commented by peter frank last updated on 26/Oct/19

$${thank}\:{you} \\ $$
Answered by malwaan last updated on 25/Oct/19
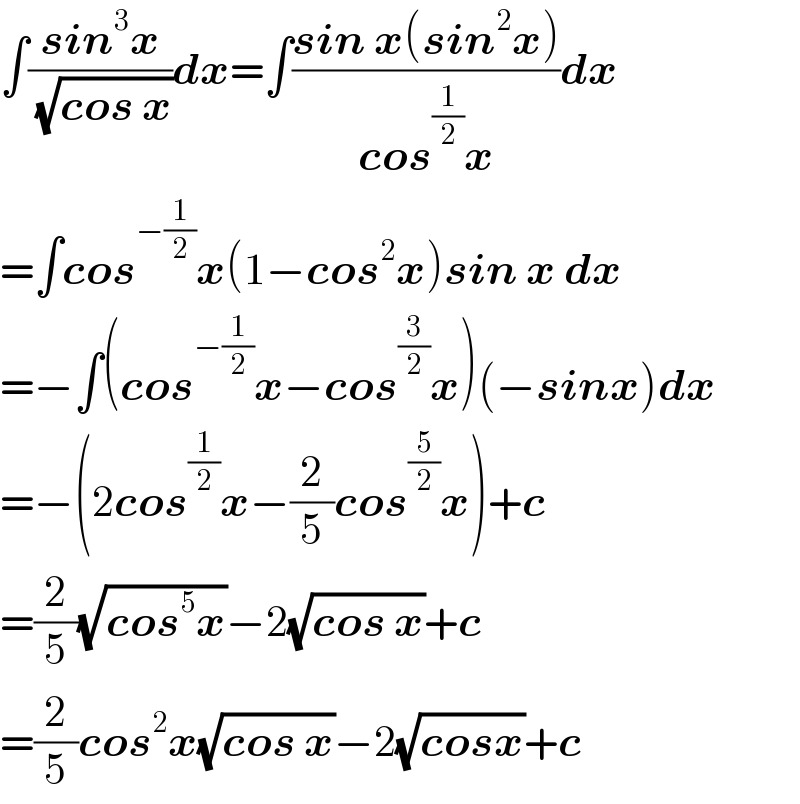
$$\int\frac{\boldsymbol{{sin}}^{\mathrm{3}} \boldsymbol{{x}}}{\:\sqrt{\boldsymbol{{cos}}\:\boldsymbol{{x}}}}\boldsymbol{{dx}}=\int\frac{\boldsymbol{{sin}}\:\boldsymbol{{x}}\left(\boldsymbol{{sin}}^{\mathrm{2}} \boldsymbol{{x}}\right)}{\boldsymbol{{cos}}^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{x}}}\boldsymbol{{dx}} \\ $$$$=\int\boldsymbol{{cos}}^{−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{x}}\left(\mathrm{1}−\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}}\right)\boldsymbol{{sin}}\:\boldsymbol{{x}}\:\boldsymbol{{dx}} \\ $$$$=−\int\left(\boldsymbol{{cos}}^{−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{x}}−\boldsymbol{{cos}}^{\frac{\mathrm{3}}{\mathrm{2}}} \boldsymbol{{x}}\right)\left(−\boldsymbol{{sinx}}\right)\boldsymbol{{dx}} \\ $$$$=−\left(\mathrm{2}\boldsymbol{{cos}}^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{x}}−\frac{\mathrm{2}}{\mathrm{5}}\boldsymbol{{cos}}^{\frac{\mathrm{5}}{\mathrm{2}}} \boldsymbol{{x}}\right)+\boldsymbol{{c}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\sqrt{\boldsymbol{{cos}}^{\mathrm{5}} \boldsymbol{{x}}}−\mathrm{2}\sqrt{\boldsymbol{{cos}}\:\boldsymbol{{x}}}+\boldsymbol{{c}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{{x}}\sqrt{\boldsymbol{{cos}}\:\boldsymbol{{x}}}−\mathrm{2}\sqrt{\boldsymbol{{cosx}}}+\boldsymbol{{c}} \\ $$
Commented by 20190927 last updated on 25/Oct/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
