Question Number 70482 by Mikaell last updated on 04/Oct/19
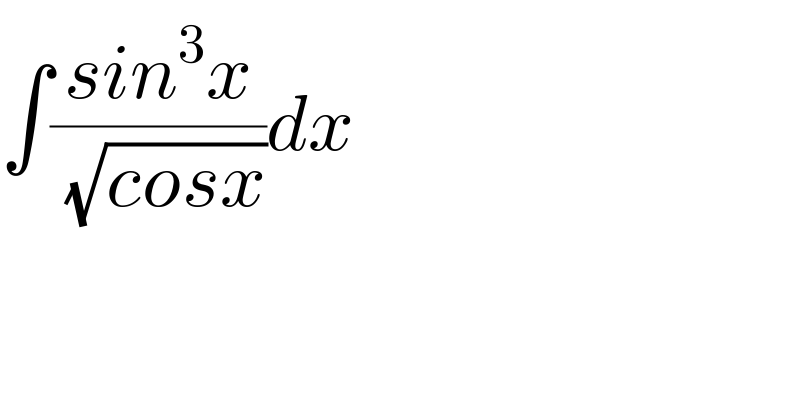
$$\int\frac{{sin}^{\mathrm{3}} {x}}{\:\sqrt{{cosx}}}{dx} \\ $$
Commented by kaivan.ahmadi last updated on 04/Oct/19
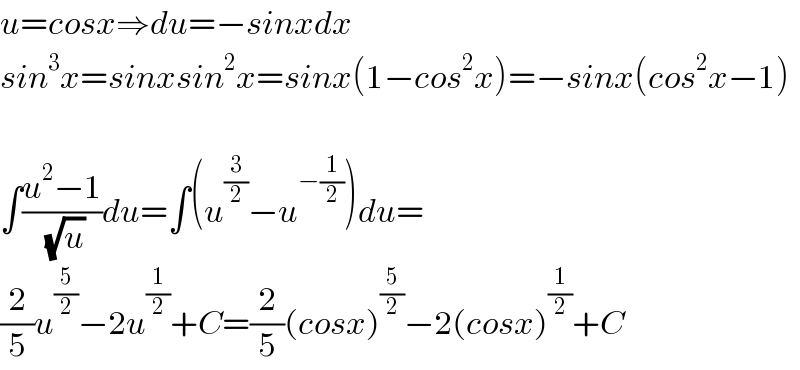
$${u}={cosx}\Rightarrow{du}=−{sinxdx} \\ $$$${sin}^{\mathrm{3}} {x}={sinxsin}^{\mathrm{2}} {x}={sinx}\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)=−{sinx}\left({cos}^{\mathrm{2}} {x}−\mathrm{1}\right) \\ $$$$ \\ $$$$\int\frac{{u}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{{u}}}{du}=\int\left({u}^{\frac{\mathrm{3}}{\mathrm{2}}} −{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \right){du}= \\ $$$$\frac{\mathrm{2}}{\mathrm{5}}{u}^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{2}{u}^{\frac{\mathrm{1}}{\mathrm{2}}} +{C}=\frac{\mathrm{2}}{\mathrm{5}}\left({cosx}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} −\mathrm{2}\left({cosx}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +{C} \\ $$
Commented by Mikaell last updated on 04/Oct/19
$${thank}\:{you}\:{Sir} \\ $$
Answered by Tanmay chaudhury last updated on 04/Oct/19
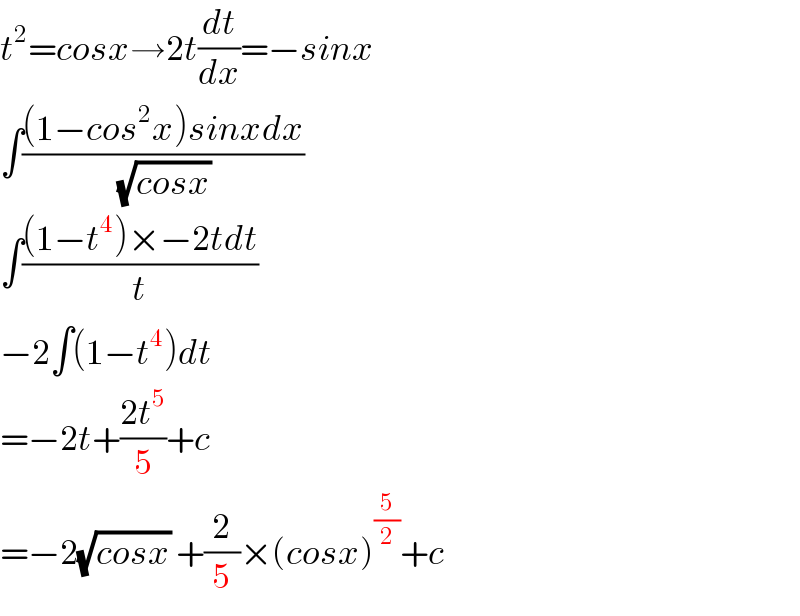
$${t}^{\mathrm{2}} ={cosx}\rightarrow\mathrm{2}{t}\frac{{dt}}{{dx}}=−{sinx} \\ $$$$\int\frac{\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){sinxdx}}{\:\sqrt{{cosx}}} \\ $$$$\int\frac{\left(\mathrm{1}−{t}^{\mathrm{4}} \right)×−\mathrm{2}{tdt}}{{t}} \\ $$$$−\mathrm{2}\int\left(\mathrm{1}−{t}^{\mathrm{4}} \right){dt} \\ $$$$=−\mathrm{2}{t}+\frac{\mathrm{2}{t}^{\mathrm{5}} }{\mathrm{5}}+{c} \\ $$$$=−\mathrm{2}\sqrt{{cosx}}\:+\frac{\mathrm{2}}{\mathrm{5}}×\left({cosx}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} +{c} \\ $$
Commented by Mikaell last updated on 04/Oct/19

$${thanks}\:{Sir} \\ $$
Commented by Prithwish sen last updated on 05/Oct/19

$$\mathrm{Sir}\:\:'\boldsymbol{\mathrm{Happy}}\:\boldsymbol{\mathrm{Durga}}\:\boldsymbol{\mathrm{Puja}}' \\ $$
Commented by Tanmay chaudhury last updated on 05/Oct/19

$${same}\:{to}\:{you}\:{sir}… \\ $$
