Question Number 142917 by ERA last updated on 07/Jun/21
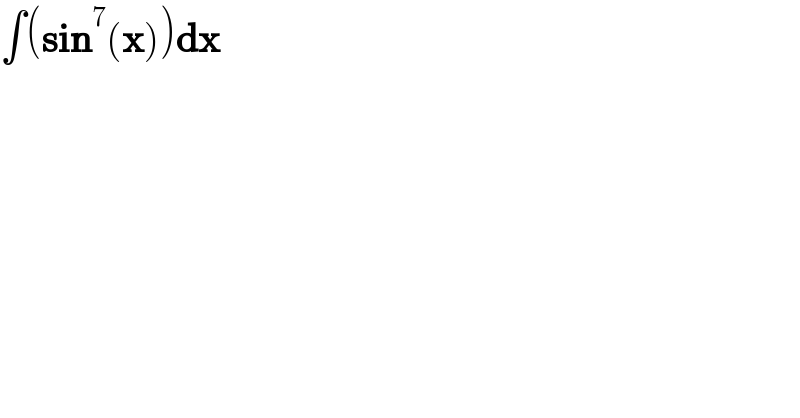
$$\int\left(\boldsymbol{\mathrm{sin}}^{\mathrm{7}} \left(\boldsymbol{\mathrm{x}}\right)\right)\boldsymbol{\mathrm{dx}} \\ $$
Answered by Ar Brandon last updated on 07/Jun/21
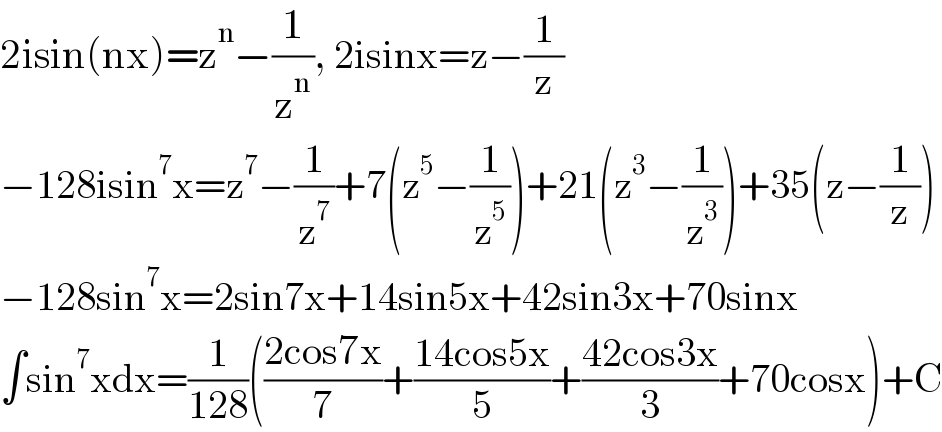
$$\mathrm{2isin}\left(\mathrm{nx}\right)=\mathrm{z}^{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} },\:\mathrm{2isinx}=\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$−\mathrm{128isin}^{\mathrm{7}} \mathrm{x}=\mathrm{z}^{\mathrm{7}} −\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{7}} }+\mathrm{7}\left(\mathrm{z}^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{5}} }\right)+\mathrm{21}\left(\mathrm{z}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{3}} }\right)+\mathrm{35}\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right) \\ $$$$−\mathrm{128sin}^{\mathrm{7}} \mathrm{x}=\mathrm{2sin7x}+\mathrm{14sin5x}+\mathrm{42sin3x}+\mathrm{70sinx} \\ $$$$\int\mathrm{sin}^{\mathrm{7}} \mathrm{xdx}=\frac{\mathrm{1}}{\mathrm{128}}\left(\frac{\mathrm{2cos7x}}{\mathrm{7}}+\frac{\mathrm{14cos5x}}{\mathrm{5}}+\frac{\mathrm{42cos3x}}{\mathrm{3}}+\mathrm{70cosx}\right)+\mathrm{C} \\ $$
