Question Number 70052 by ahmadshahhimat775@gmail.com last updated on 30/Sep/19

$$ \\ $$$$\mathrm{sin}\:{A}+\mathrm{sin}\:{B}={n}\:\:\:\:\:\:\:\:\:{and}\:\:\:\:\:\:\:\:\mathrm{cos}\:{A}+\mathrm{cos}\:{B}={m} \\ $$$$\mathrm{sin}\:\left({A}+{B}\right)=? \\ $$
Answered by $@ty@m123 last updated on 30/Sep/19
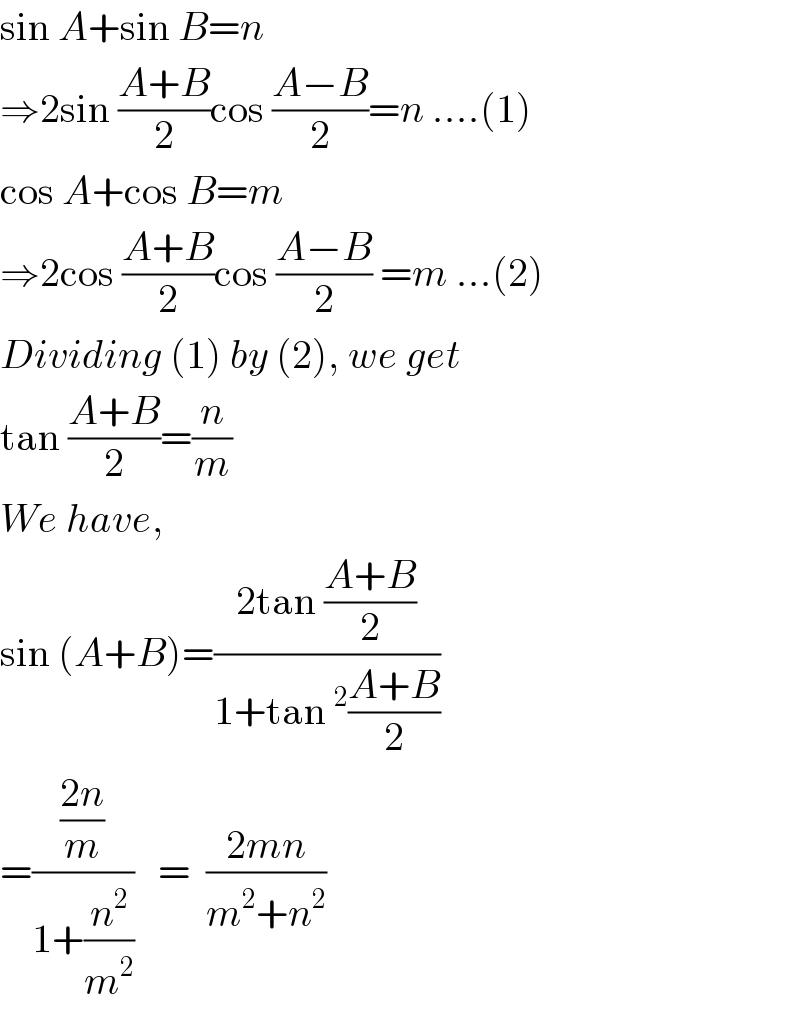
$$\mathrm{sin}\:{A}+\mathrm{sin}\:{B}={n} \\ $$$$\Rightarrow\mathrm{2sin}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}={n}\:….\left(\mathrm{1}\right) \\ $$$$\mathrm{cos}\:{A}+\mathrm{cos}\:{B}={m} \\ $$$$\Rightarrow\mathrm{2cos}\:\frac{{A}+{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{A}−{B}}{\mathrm{2}}\:={m}\:…\left(\mathrm{2}\right) \\ $$$${Dividing}\:\left(\mathrm{1}\right)\:{by}\:\left(\mathrm{2}\right),\:{we}\:{get} \\ $$$$\mathrm{tan}\:\frac{{A}+{B}}{\mathrm{2}}=\frac{{n}}{{m}} \\ $$$${We}\:{have}, \\ $$$$\mathrm{sin}\:\left({A}+{B}\right)=\frac{\mathrm{2tan}\:\frac{{A}+{B}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \frac{{A}+{B}}{\mathrm{2}}} \\ $$$$=\frac{\frac{\mathrm{2}{n}}{{m}}}{\mathrm{1}+\frac{{n}^{\mathrm{2}} }{{m}^{\mathrm{2}} }}\:\:\:=\:\:\frac{\mathrm{2}{mn}}{{m}^{\mathrm{2}} +{n}^{\mathrm{2}} } \\ $$
