Menu Close

sin-x-3-c-dx-sinh-x-3-c-dx-

Tinku Tara 0 Comments
Pin




Question Number 75089 by MJS last updated on 07/Dec/19
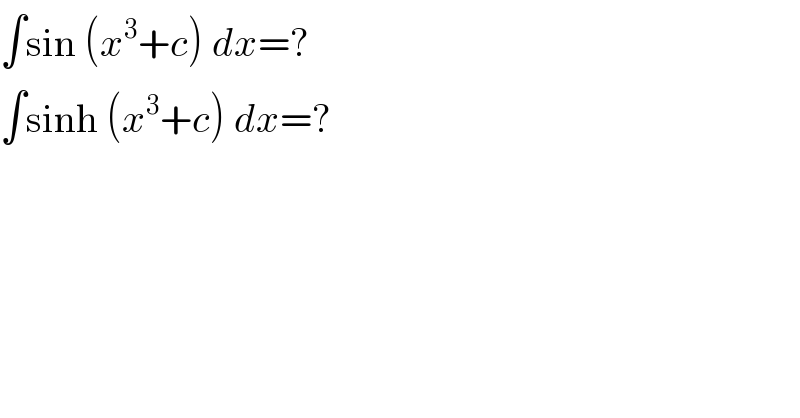
∫sin (x^3 +c) dx=? ∫sinh (x^3 +c) dx=?
$$\int\mathrm{sin}\:\left({x}^{\mathrm{3}} +{c}\right)\:{dx}=? \\ $$$$\int\mathrm{sinh}\:\left({x}^{\mathrm{3}} +{c}\right)\:{dx}=? \\ $$
Commented by mathmax by abdo last updated on 07/Dec/19
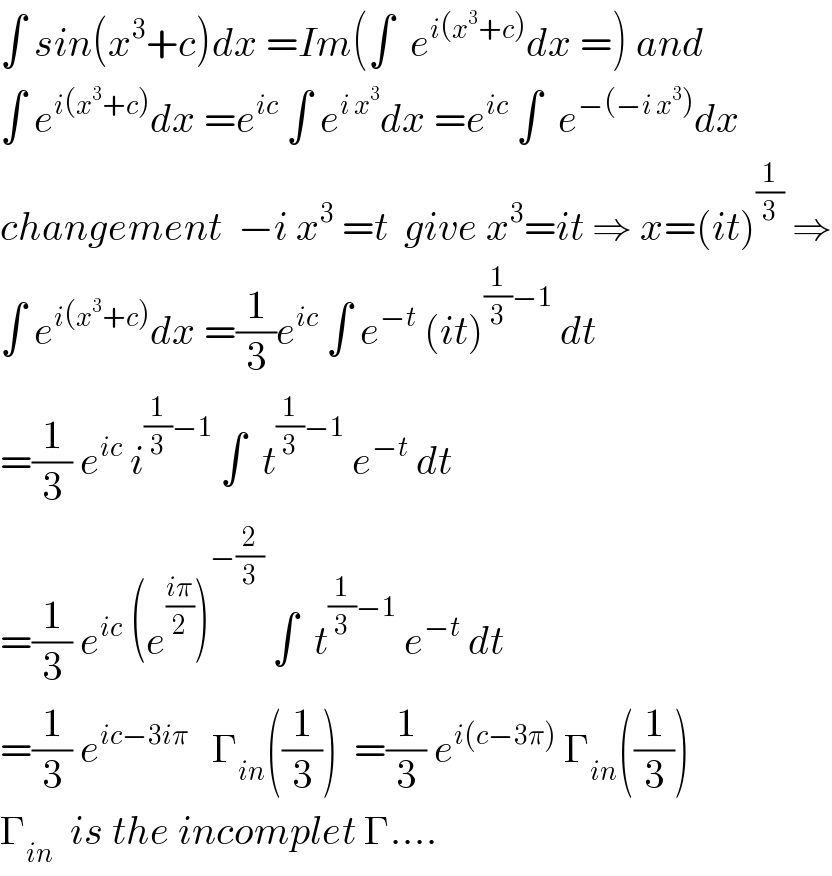
∫ sin(x^3 +c)dx =Im(∫ e^(i(x^3 +c)) dx =) and ∫ e^(i(x^3 +c)) dx =e^(ic) ∫ e^(i x^3 ) dx =e^(ic) ∫ e^(−(−i x^3 )) dx changement −i x^3 =t give x^3 =it ⇒ x=(it)^(1/3) ⇒ ∫ e^(i(x^3 +c)) dx =(1/3)e^(ic) ∫ e^(−t) (it)^((1/3)−1) dt =(1/3) e^(ic) i^((1/3)−1) ∫ t^((1/3)−1) e^(−t) dt =(1/3) e^(ic) (e^((iπ)/2) )^(−(2/3)) ∫ t^((1/3)−1) e^(−t) dt =(1/3) e^(ic−3iπ) Γ_(in) ((1/3)) =(1/3) e^(i(c−3π)) Γ_(in) ((1/3)) Γ_(in) is the incomplet Γ....
$$\int\:{sin}\left({x}^{\mathrm{3}} +{c}\right){dx}\:={Im}\left(\int\:\:{e}^{{i}\left({x}^{\mathrm{3}} +{c}\right)} {dx}\:=\right)\:{and} \\ $$$$\int\:{e}^{{i}\left({x}^{\mathrm{3}} +{c}\right)} {dx}\:={e}^{{ic}} \:\int\:{e}^{{i}\:{x}^{\mathrm{3}} } {dx}\:={e}^{{ic}} \:\int\:\:{e}^{−\left(−{i}\:{x}^{\mathrm{3}} \right)} {dx} \\ $$$${changement}\:\:−{i}\:{x}^{\mathrm{3}} \:={t}\:\:{give}\:{x}^{\mathrm{3}} ={it}\:\Rightarrow\:{x}=\left({it}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\int\:{e}^{{i}\left({x}^{\mathrm{3}} +{c}\right)} {dx}\:=\frac{\mathrm{1}}{\mathrm{3}}{e}^{{ic}} \:\int\:{e}^{−{t}} \:\left({it}\right)^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{{ic}} \:{i}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:\int\:\:{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{e}^{−{t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{{ic}} \:\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:\int\:\:{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{e}^{−{t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{{ic}−\mathrm{3}{i}\pi} \:\:\:\Gamma_{{in}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\:=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{{i}\left({c}−\mathrm{3}\pi\right)} \:\Gamma_{{in}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Gamma_{{in}} \:\:{is}\:{the}\:{incomplet}\:\Gamma…. \\ $$
Commented by mathmax by abdo last updated on 07/Dec/19
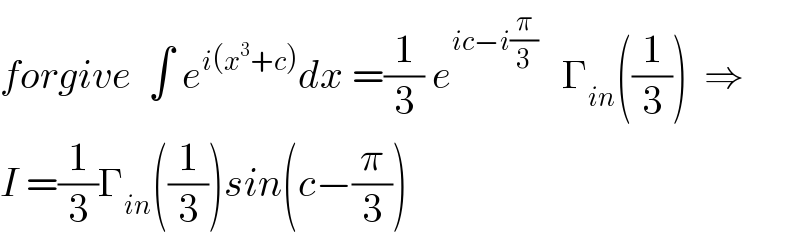
forgive ∫ e^(i(x^3 +c)) dx =(1/3) e^(ic−i(π/3)) Γ_(in) ((1/3)) ⇒ I =(1/3)Γ_(in) ((1/3))sin(c−(π/3))
$${forgive}\:\:\int\:{e}^{{i}\left({x}^{\mathrm{3}} +{c}\right)} {dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{{ic}−{i}\frac{\pi}{\mathrm{3}}} \:\:\:\Gamma_{{in}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\:\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{3}}\Gamma_{{in}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right){sin}\left({c}−\frac{\pi}{\mathrm{3}}\right) \\ $$
Commented by MJS last updated on 07/Dec/19
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mathmax by abdo last updated on 14/Dec/19
you are welcome sir.
$${you}\:{are}\:{welcome}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *