Question Number 4429 by alib last updated on 24/Jan/16
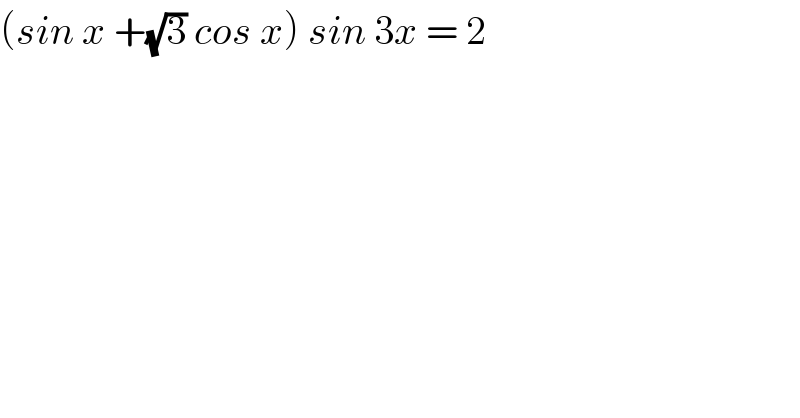
$$\left({sin}\:{x}\:+\sqrt{\mathrm{3}}\:{cos}\:{x}\right)\:{sin}\:\mathrm{3}{x}\:=\:\mathrm{2} \\ $$
Answered by Yozzii last updated on 24/Jan/16
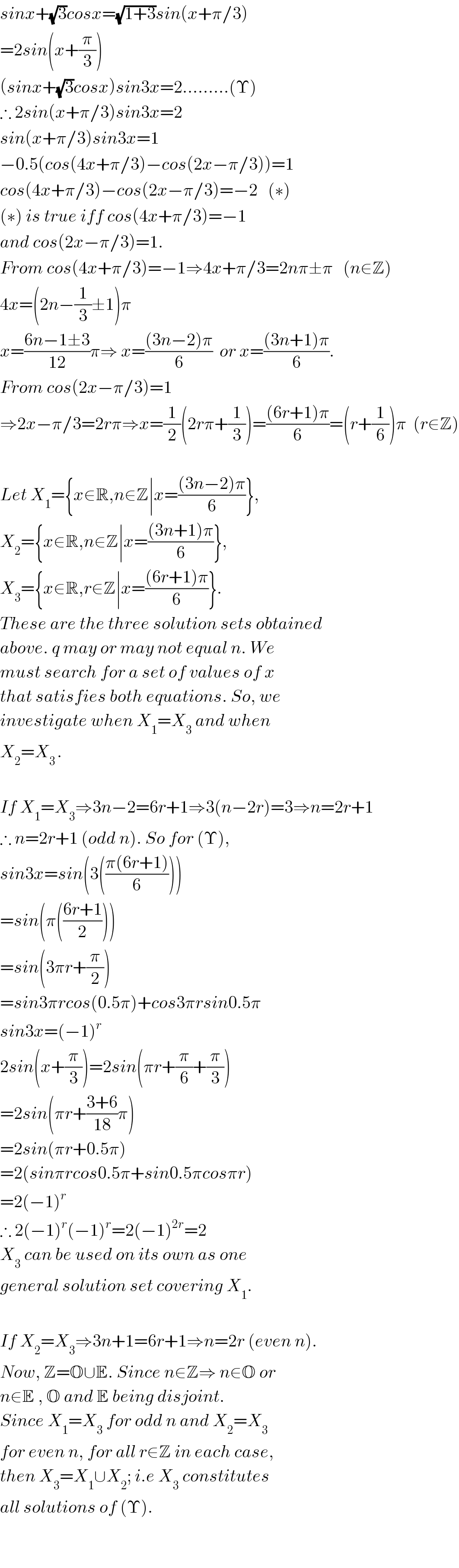
$${sinx}+\sqrt{\mathrm{3}}{cosx}=\sqrt{\mathrm{1}+\mathrm{3}}{sin}\left({x}+\pi/\mathrm{3}\right) \\ $$$$=\mathrm{2}{sin}\left({x}+\frac{\pi}{\mathrm{3}}\right) \\ $$$$\left({sinx}+\sqrt{\mathrm{3}}{cosx}\right){sin}\mathrm{3}{x}=\mathrm{2}………\left(\Upsilon\right) \\ $$$$\therefore\:\mathrm{2}{sin}\left({x}+\pi/\mathrm{3}\right){sin}\mathrm{3}{x}=\mathrm{2} \\ $$$${sin}\left({x}+\pi/\mathrm{3}\right){sin}\mathrm{3}{x}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\: \\ $$$$−\mathrm{0}.\mathrm{5}\left({cos}\left(\mathrm{4}{x}+\pi/\mathrm{3}\right)−{cos}\left(\mathrm{2}{x}−\pi/\mathrm{3}\right)\right)=\mathrm{1} \\ $$$${cos}\left(\mathrm{4}{x}+\pi/\mathrm{3}\right)−{cos}\left(\mathrm{2}{x}−\pi/\mathrm{3}\right)=−\mathrm{2}\:\:\:\left(\ast\right) \\ $$$$\left(\ast\right)\:{is}\:{true}\:{iff}\:{cos}\left(\mathrm{4}{x}+\pi/\mathrm{3}\right)=−\mathrm{1} \\ $$$${and}\:{cos}\left(\mathrm{2}{x}−\pi/\mathrm{3}\right)=\mathrm{1}. \\ $$$${From}\:{cos}\left(\mathrm{4}{x}+\pi/\mathrm{3}\right)=−\mathrm{1}\Rightarrow\mathrm{4}{x}+\pi/\mathrm{3}=\mathrm{2}{n}\pi\pm\pi\:\:\:\left({n}\in\mathbb{Z}\right) \\ $$$$\mathrm{4}{x}=\left(\mathrm{2}{n}−\frac{\mathrm{1}}{\mathrm{3}}\pm\mathrm{1}\right)\pi \\ $$$${x}=\frac{\mathrm{6}{n}−\mathrm{1}\pm\mathrm{3}}{\mathrm{12}}\pi\Rightarrow\:{x}=\frac{\left(\mathrm{3}{n}−\mathrm{2}\right)\pi}{\mathrm{6}}\:\:{or}\:{x}=\frac{\left(\mathrm{3}{n}+\mathrm{1}\right)\pi}{\mathrm{6}}. \\ $$$${From}\:{cos}\left(\mathrm{2}{x}−\pi/\mathrm{3}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}{x}−\pi/\mathrm{3}=\mathrm{2}{r}\pi\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{r}\pi+\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\left(\mathrm{6}{r}+\mathrm{1}\right)\pi}{\mathrm{6}}=\left({r}+\frac{\mathrm{1}}{\mathrm{6}}\right)\pi\:\:\left({r}\in\mathbb{Z}\right) \\ $$$$ \\ $$$${Let}\:{X}_{\mathrm{1}} =\left\{{x}\in\mathbb{R},{n}\in\mathbb{Z}\mid{x}=\frac{\left(\mathrm{3}{n}−\mathrm{2}\right)\pi}{\mathrm{6}}\right\}, \\ $$$${X}_{\mathrm{2}} =\left\{{x}\in\mathbb{R},{n}\in\mathbb{Z}\mid{x}=\frac{\left(\mathrm{3}{n}+\mathrm{1}\right)\pi}{\mathrm{6}}\right\}, \\ $$$${X}_{\mathrm{3}} =\left\{{x}\in\mathbb{R},{r}\in\mathbb{Z}\mid{x}=\frac{\left(\mathrm{6}{r}+\mathrm{1}\right)\pi}{\mathrm{6}}\right\}. \\ $$$${These}\:{are}\:{the}\:{three}\:{solution}\:{sets}\:{obtained} \\ $$$${above}.\:{q}\:{may}\:{or}\:{may}\:{not}\:{equal}\:{n}.\:{We} \\ $$$${must}\:{search}\:{for}\:{a}\:{set}\:{of}\:{values}\:{of}\:{x} \\ $$$${that}\:{satisfies}\:{both}\:{equations}.\:{So},\:{we}\: \\ $$$${investigate}\:{when}\:{X}_{\mathrm{1}} ={X}_{\mathrm{3}} \:{and}\:{when} \\ $$$${X}_{\mathrm{2}} ={X}_{\mathrm{3}\:} . \\ $$$$ \\ $$$${If}\:{X}_{\mathrm{1}} ={X}_{\mathrm{3}} \Rightarrow\mathrm{3}{n}−\mathrm{2}=\mathrm{6}{r}+\mathrm{1}\Rightarrow\mathrm{3}\left({n}−\mathrm{2}{r}\right)=\mathrm{3}\Rightarrow{n}=\mathrm{2}{r}+\mathrm{1} \\ $$$$\therefore\:{n}=\mathrm{2}{r}+\mathrm{1}\:\left({odd}\:{n}\right).\:{So}\:{for}\:\left(\Upsilon\right), \\ $$$${sin}\mathrm{3}{x}={sin}\left(\mathrm{3}\left(\frac{\pi\left(\mathrm{6}{r}+\mathrm{1}\right)}{\mathrm{6}}\right)\right) \\ $$$$={sin}\left(\pi\left(\frac{\mathrm{6}{r}+\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$={sin}\left(\mathrm{3}\pi{r}+\frac{\pi}{\mathrm{2}}\right) \\ $$$$={sin}\mathrm{3}\pi{rcos}\left(\mathrm{0}.\mathrm{5}\pi\right)+{cos}\mathrm{3}\pi{rsin}\mathrm{0}.\mathrm{5}\pi \\ $$$${sin}\mathrm{3}{x}=\left(−\mathrm{1}\right)^{{r}} \\ $$$$\mathrm{2}{sin}\left({x}+\frac{\pi}{\mathrm{3}}\right)=\mathrm{2}{sin}\left(\pi{r}+\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{2}{sin}\left(\pi{r}+\frac{\mathrm{3}+\mathrm{6}}{\mathrm{18}}\pi\right) \\ $$$$=\mathrm{2}{sin}\left(\pi{r}+\mathrm{0}.\mathrm{5}\pi\right) \\ $$$$=\mathrm{2}\left({sin}\pi{rcos}\mathrm{0}.\mathrm{5}\pi+{sin}\mathrm{0}.\mathrm{5}\pi{cos}\pi{r}\right) \\ $$$$=\mathrm{2}\left(−\mathrm{1}\right)^{{r}} \\ $$$$\therefore\:\mathrm{2}\left(−\mathrm{1}\right)^{{r}} \left(−\mathrm{1}\right)^{{r}} =\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{2}{r}} =\mathrm{2}\:\:\:\: \\ $$$${X}_{\mathrm{3}} \:{can}\:{be}\:{used}\:{on}\:{its}\:{own}\:{as}\:{one}\: \\ $$$${general}\:{solution}\:{set}\:{covering}\:{X}_{\mathrm{1}} . \\ $$$$ \\ $$$${If}\:{X}_{\mathrm{2}} ={X}_{\mathrm{3}} \Rightarrow\mathrm{3}{n}+\mathrm{1}=\mathrm{6}{r}+\mathrm{1}\Rightarrow{n}=\mathrm{2}{r}\:\left({even}\:{n}\right). \\ $$$${Now},\:\mathbb{Z}=\mathbb{O}\cup\mathbb{E}.\:{Since}\:{n}\in\mathbb{Z}\Rightarrow\:{n}\in\mathbb{O}\:{or} \\ $$$${n}\in\mathbb{E}\:,\:\mathbb{O}\:{and}\:\mathbb{E}\:{being}\:{disjoint}.\: \\ $$$${Since}\:{X}_{\mathrm{1}} ={X}_{\mathrm{3}} \:{for}\:{odd}\:{n}\:{and}\:{X}_{\mathrm{2}} ={X}_{\mathrm{3}} \\ $$$${for}\:{even}\:{n},\:{for}\:{all}\:{r}\in\mathbb{Z}\:{in}\:{each}\:{case}, \\ $$$${then}\:{X}_{\mathrm{3}} ={X}_{\mathrm{1}} \cup{X}_{\mathrm{2}} ;\:{i}.{e}\:{X}_{\mathrm{3}} \:{constitutes} \\ $$$${all}\:{solutions}\:{of}\:\left(\Upsilon\right). \\ $$$$ \\ $$$$ \\ $$
