Question Number 11456 by Joel576 last updated on 26/Mar/17
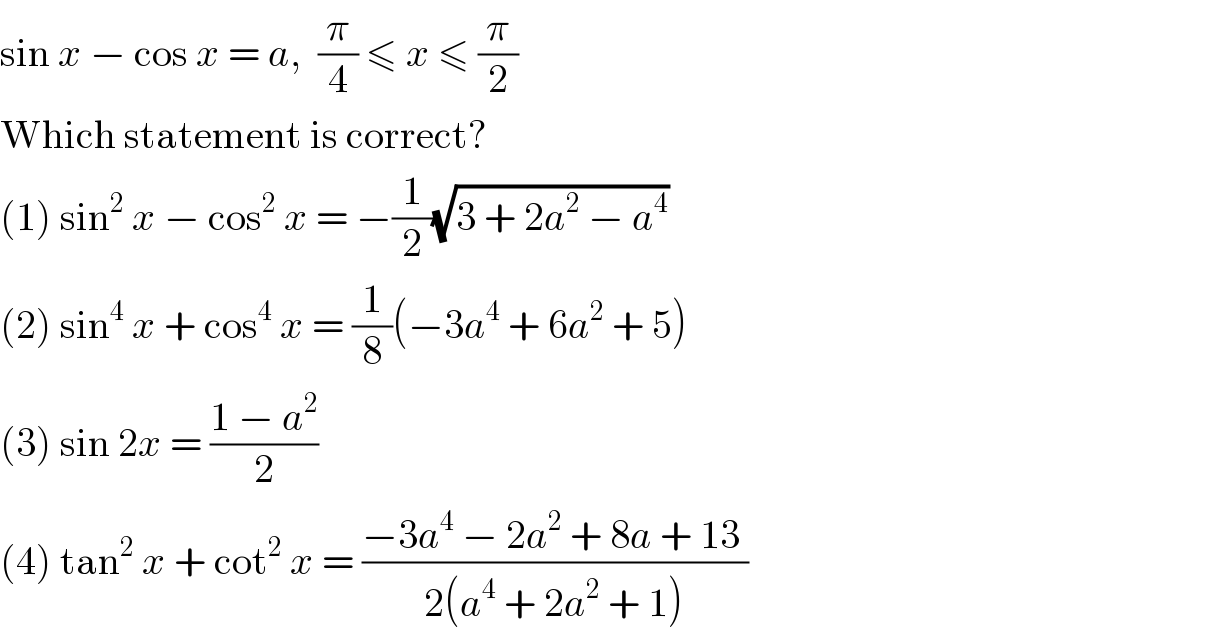
$$\mathrm{sin}\:{x}\:−\:\mathrm{cos}\:{x}\:=\:{a},\:\:\frac{\pi}{\mathrm{4}}\:\leqslant\:{x}\:\leqslant\:\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{Which}\:\mathrm{statement}\:\mathrm{is}\:\mathrm{correct}? \\ $$$$\left(\mathrm{1}\right)\:\mathrm{sin}^{\mathrm{2}} \:{x}\:−\:\mathrm{cos}^{\mathrm{2}} \:{x}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}\:+\:\mathrm{2}{a}^{\mathrm{2}} \:−\:{a}^{\mathrm{4}} } \\ $$$$\left(\mathrm{2}\right)\:\mathrm{sin}^{\mathrm{4}} \:{x}\:+\:\mathrm{cos}^{\mathrm{4}} \:{x}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(−\mathrm{3}{a}^{\mathrm{4}} \:+\:\mathrm{6}{a}^{\mathrm{2}} \:+\:\mathrm{5}\right) \\ $$$$\left(\mathrm{3}\right)\:\mathrm{sin}\:\mathrm{2}{x}\:=\:\frac{\mathrm{1}\:−\:{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{tan}^{\mathrm{2}} \:{x}\:+\:\mathrm{cot}^{\mathrm{2}} \:{x}\:=\:\frac{−\mathrm{3}{a}^{\mathrm{4}} \:−\:\mathrm{2}{a}^{\mathrm{2}} \:+\:\mathrm{8}{a}\:+\:\mathrm{13}\:}{\mathrm{2}\left({a}^{\mathrm{4}} \:+\:\mathrm{2}{a}^{\mathrm{2}} \:+\:\mathrm{1}\right)} \\ $$
Commented by ajfour last updated on 26/Mar/17
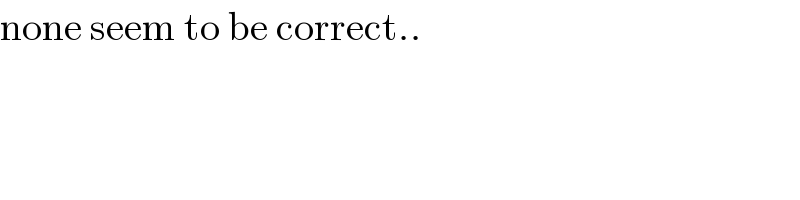
$$\mathrm{none}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{be}\:\mathrm{correct}.. \\ $$
Commented by Joel576 last updated on 26/Mar/17

$${why}? \\ $$
Commented by Joel576 last updated on 26/Mar/17
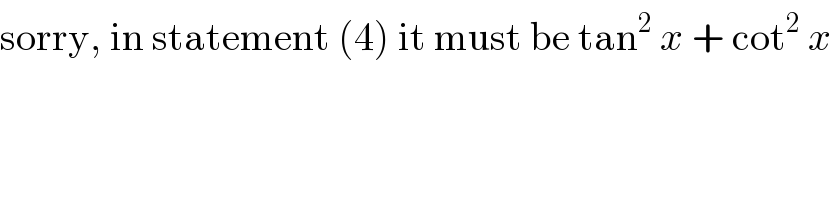
$$\mathrm{sorry},\:\mathrm{in}\:\mathrm{statement}\:\left(\mathrm{4}\right)\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{tan}^{\mathrm{2}} \:{x}\:+\:\mathrm{cot}^{\mathrm{2}} \:{x} \\ $$
Answered by ridwan balatif last updated on 26/Mar/17
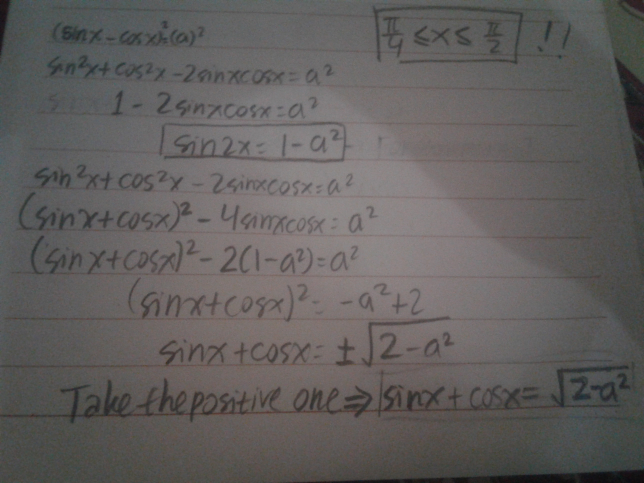
Answered by ridwan balatif last updated on 26/Mar/17

Commented by Joel576 last updated on 27/Mar/17
$${thank}\:{you}\:{very}\:{much} \\ $$
