Question Number 140907 by bramlexs22 last updated on 14/May/21

$$\:\sqrt{\mathrm{sin}\:\mathrm{x}}\:\mathrm{cos}\:\mathrm{x}\:−\sqrt{\mathrm{sin}\:^{\mathrm{5}} \mathrm{x}}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\:\sqrt{\mathrm{sin}\:\mathrm{x}} \\ $$
Answered by john_santu last updated on 14/May/21
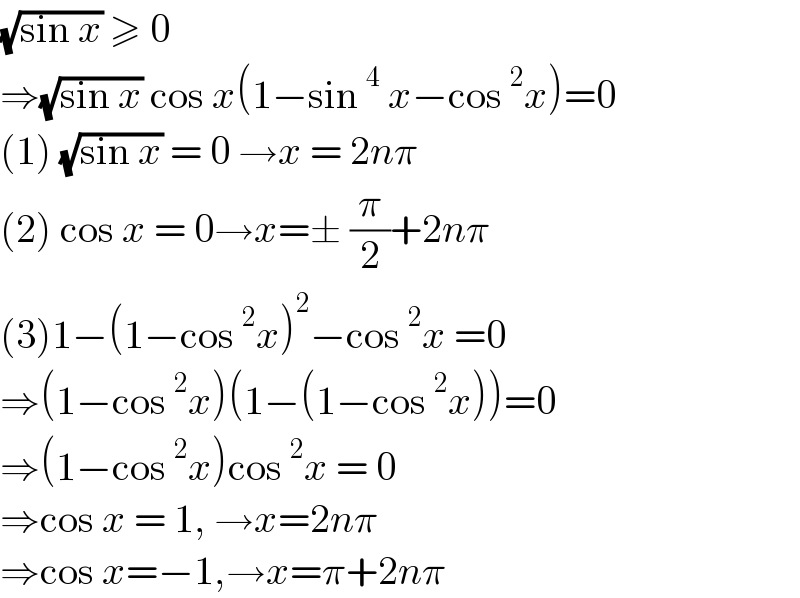
$$\sqrt{\mathrm{sin}\:{x}}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\sqrt{\mathrm{sin}\:{x}}\:\mathrm{cos}\:{x}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{4}} \:{x}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\sqrt{\mathrm{sin}\:{x}}\:=\:\mathrm{0}\:\rightarrow{x}\:=\:\mathrm{2}{n}\pi \\ $$$$\left(\mathrm{2}\right)\:\mathrm{cos}\:{x}\:=\:\mathrm{0}\rightarrow{x}=\pm\:\frac{\pi}{\mathrm{2}}+\mathrm{2}{n}\pi \\ $$$$\left(\mathrm{3}\right)\mathrm{1}−\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{cos}\:^{\mathrm{2}} {x}\:=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)\left(\mathrm{1}−\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)\mathrm{cos}\:^{\mathrm{2}} {x}\:=\:\mathrm{0} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\:=\:\mathrm{1},\:\rightarrow{x}=\mathrm{2}{n}\pi \\ $$$$\Rightarrow\mathrm{cos}\:{x}=−\mathrm{1},\rightarrow{x}=\pi+\mathrm{2}{n}\pi\: \\ $$
