Menu Close

sin-x-cos-x-x-sin-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 137509 by liberty last updated on 03/Apr/21
∫ ((sin ((√x) )+cos ((√x) ))/( (√x) sin (2(√x) ))) dx
$$\int\:\frac{\mathrm{sin}\:\left(\sqrt{{x}}\:\right)+\mathrm{cos}\:\left(\sqrt{{x}}\:\right)}{\:\sqrt{{x}}\:\mathrm{sin}\:\left(\mathrm{2}\sqrt{{x}}\:\right)}\:{dx}\: \\ $$
Commented by liberty last updated on 04/Apr/21
Answered by Ñï= last updated on 03/Apr/21
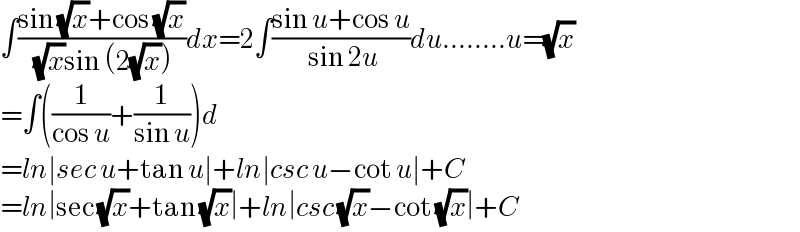
∫((sin (√x)+cos (√x))/( (√x)sin (2(√x))))dx=2∫((sin u+cos u)/( sin 2u))du........u=(√x) =∫((1/(cos u))+(1/(sin u)))d =ln∣sec u+tan u∣+ln∣csc u−cot u∣+C =ln∣sec (√x)+tan (√x)∣+ln∣csc (√x)−cot (√x)∣+C
$$\int\frac{\mathrm{sin}\:\sqrt{{x}}+\mathrm{cos}\:\sqrt{{x}}}{\:\sqrt{{x}}\mathrm{sin}\:\left(\mathrm{2}\sqrt{{x}}\right)}{dx}=\mathrm{2}\int\frac{\mathrm{sin}\:{u}+\mathrm{cos}\:{u}}{\:\mathrm{sin}\:\mathrm{2}{u}}{du}……..{u}=\sqrt{{x}} \\ $$$$=\int\left(\frac{\mathrm{1}}{\mathrm{cos}\:{u}}+\frac{\mathrm{1}}{\mathrm{sin}\:{u}}\right){d} \\ $$$$={ln}\mid{sec}\:{u}+\mathrm{tan}\:{u}\mid+{ln}\mid{csc}\:{u}−\mathrm{cot}\:{u}\mid+{C} \\ $$$$={ln}\mid\mathrm{sec}\:\sqrt{{x}}+\mathrm{tan}\:\sqrt{{x}}\mid+{ln}\mid{csc}\:\sqrt{{x}}−\mathrm{cot}\:\sqrt{{x}}\mid+{C} \\ $$
Answered by mathmax by abdo last updated on 03/Apr/21
I=∫ ((sin((√x))+cos((√x)))/( (√x)sin(2(√x))))dx ⇒I=_((√x)=t) ∫ ((sint+cost)/(tsin(2t)))(2t)dt =2∫ ((sint +cost)/(2sint .cost))dt =∫ (dt/(cost))+∫ (dt/(sint)) changement tan((t/2))=y give ∫ (dt/(cost)) =∫ ((2dy)/((1+y^2 )((1−y^2 )/(1+y^2 )))) =2∫ (dy/((1−y)(1+y))) =∫ ((1/(1−y))+(1/(1+y)))dy =log∣((1+y)/(1−y))∣ +c_1 =log∣((1+tan(((√x)/2)))/(1−tan(((√x)/2))))∣+c_1 ∫ (dt/(sint)) =∫ ((2dy)/((1+y^2 ).((2y)/(1+y^2 )))) =∫ (dy/y)=log∣y∣ +c_2 =log∣tan(((√x)/2))∣ +c_2 ⇒ I =log∣((1+tan(((√x)/2)))/(1−tan(((√x)/2))))∣+log∣tan(((√x)/2))∣ +C
$$\mathrm{I}=\int\:\:\frac{\mathrm{sin}\left(\sqrt{\mathrm{x}}\right)+\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)}{\:\sqrt{\mathrm{x}}\mathrm{sin}\left(\mathrm{2}\sqrt{\mathrm{x}}\right)}\mathrm{dx}\:\Rightarrow\mathrm{I}=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int\:\:\frac{\mathrm{sint}+\mathrm{cost}}{\mathrm{tsin}\left(\mathrm{2t}\right)}\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int\:\:\:\frac{\mathrm{sint}\:+\mathrm{cost}}{\mathrm{2sint}\:.\mathrm{cost}}\mathrm{dt}\:=\int\:\frac{\mathrm{dt}}{\mathrm{cost}}+\int\:\:\frac{\mathrm{dt}}{\mathrm{sint}} \\ $$$$\mathrm{changement}\:\:\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{y}\:\mathrm{give}\:\int\:\frac{\mathrm{dt}}{\mathrm{cost}}\:=\int\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }} \\ $$$$=\mathrm{2}\int\:\:\frac{\mathrm{dy}}{\left(\mathrm{1}−\mathrm{y}\right)\left(\mathrm{1}+\mathrm{y}\right)}\:=\int\:\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{y}}+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{y}}\right)\mathrm{dy}\:=\mathrm{log}\mid\frac{\mathrm{1}+\mathrm{y}}{\mathrm{1}−\mathrm{y}}\mid\:+\mathrm{c}_{\mathrm{1}} \\ $$$$=\mathrm{log}\mid\frac{\mathrm{1}+\mathrm{tan}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)}\mid+\mathrm{c}_{\mathrm{1}} \\ $$$$\int\:\:\frac{\mathrm{dt}}{\mathrm{sint}}\:=\int\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right).\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }}\:=\int\:\frac{\mathrm{dy}}{\mathrm{y}}=\mathrm{log}\mid\mathrm{y}\mid\:+\mathrm{c}_{\mathrm{2}} \\ $$$$=\mathrm{log}\mid\mathrm{tan}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)\mid\:+\mathrm{c}_{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{log}\mid\frac{\mathrm{1}+\mathrm{tan}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)}\mid+\mathrm{log}\mid\mathrm{tan}\left(\frac{\sqrt{\mathrm{x}}}{\mathrm{2}}\right)\mid\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *