sin1-sin2-2-sin3-3-sin4-4-1-2-

Question Number 134439 by Dwaipayan Shikari last updated on 03/Mar/21

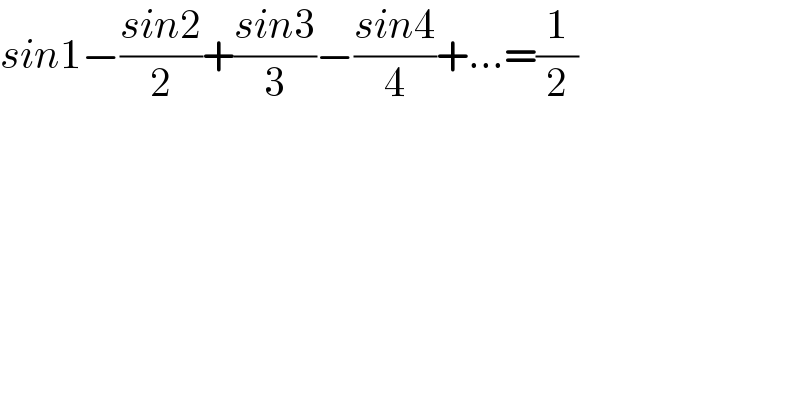
$${sin}\mathrm{1}−\frac{{sin}\mathrm{2}}{\mathrm{2}}+\frac{{sin}\mathrm{3}}{\mathrm{3}}−\frac{{sin}\mathrm{4}}{\mathrm{4}}+…=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by mnjuly1970 last updated on 03/Mar/21

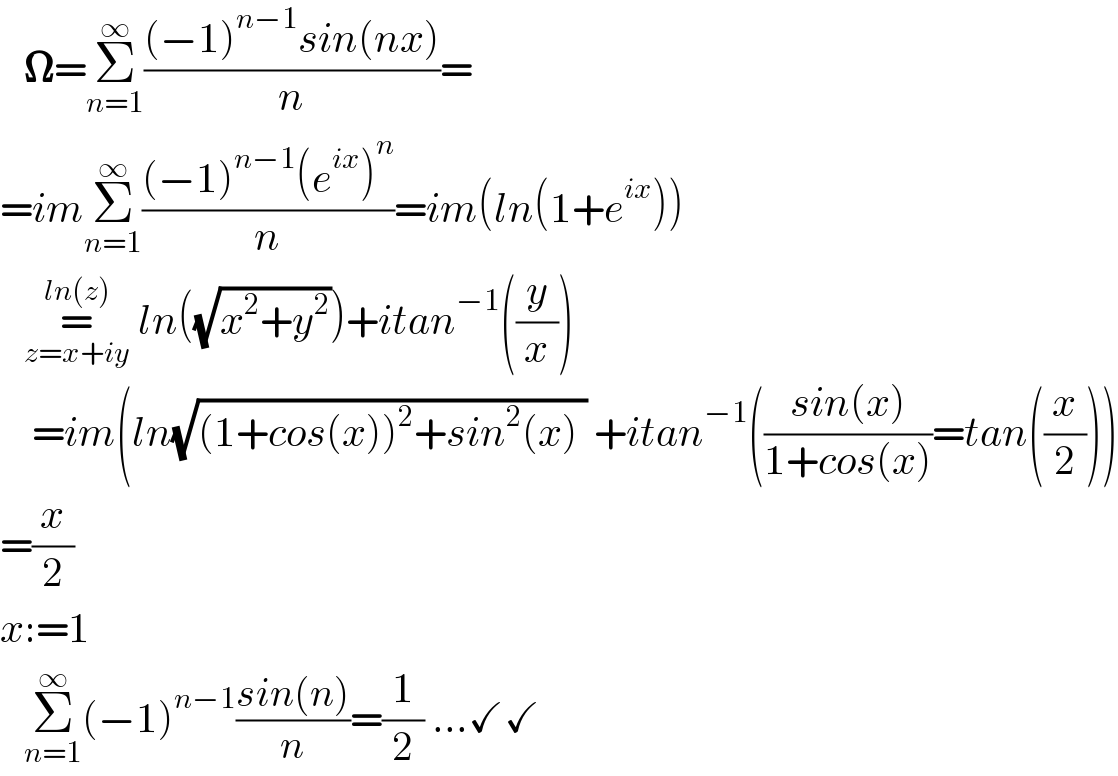
𝛀=Σ_(n=1) ^∞ (((−1)^(n−1) sin(nx))/n)= =imΣ_(n=1) ^∞ (((−1)^(n−1) (e^(ix) )^n )/n)=im(ln(1+e^(ix) )) =_(z=x+iy) ^(ln(z)) ln((√(x^2 +y^2 )))+itan^(−1) ((y/x)) =im(ln(√((1+cos(x))^2 +sin^2 (x) )) +itan^(−1) (((sin(x))/(1+cos(x)))=tan((x/2))) =(x/2) x:=1 Σ_(n=1) ^∞ (−1)^(n−1) ((sin(n))/n)=(1/2) ...✓✓

$$\:\:\:\boldsymbol{\Omega}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {sin}\left({nx}\right)}{{n}}=\:\:\: \\ $$$$={im}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({e}^{{ix}} \right)^{{n}} }{{n}}={im}\left({ln}\left(\mathrm{1}+{e}^{{ix}} \right)\right) \\ $$$$\:\:\:\underset{{z}={x}+{iy}} {\overset{{ln}\left({z}\right)} {=}}\:{ln}\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)+{itan}^{−\mathrm{1}} \left(\frac{{y}}{{x}}\right) \\ $$$$\:\:\:\:={im}\left({ln}\sqrt{\left(\mathrm{1}+{cos}\left({x}\right)\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \left({x}\right)\:}\:+{itan}^{−\mathrm{1}} \left(\frac{{sin}\left({x}\right)}{\mathrm{1}+{cos}\left({x}\right)}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)\right. \\ $$$$=\frac{{x}}{\mathrm{2}} \\ $$$${x}:=\mathrm{1} \\ $$$$\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{{sin}\left({n}\right)}{{n}}=\frac{\mathrm{1}}{\mathrm{2}}\:…\checkmark\checkmark \\ $$

Commented by Dwaipayan Shikari last updated on 03/Mar/21

Great sir! It is simple and nice. (x/2)=sinx−((sin2x)/2)+((sin3x)/3)−((sin4x)/4)+... (0<x<π) But ,Differentiating respect to x (1/2)=cosx−cos2x+cos3x−cos4x+.... (Independent of x!) Is it true? If we take x=0 (1/2)=1−1+1−1+1−1+.... But 0<x<π

$${Great}\:{sir}!\:{It}\:{is}\:{simple}\:{and}\:{nice}. \\ $$$$\frac{{x}}{\mathrm{2}}={sinx}−\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}+\frac{{sin}\mathrm{3}{x}}{\mathrm{3}}−\frac{{sin}\mathrm{4}{x}}{\mathrm{4}}+…\:\:\left(\mathrm{0}<{x}<\pi\right) \\ $$$${But}\:,{Differentiating}\:{respect}\:{to}\:{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}={cosx}−{cos}\mathrm{2}{x}+{cos}\mathrm{3}{x}−{cos}\mathrm{4}{x}+….\:\:\:\left({Independent}\:{of}\:{x}!\right) \\ $$$${Is}\:{it}\:{true}? \\ $$$${If}\:{we}\:{take}\:{x}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+\mathrm{1}−\mathrm{1}+….\: \\ $$$${But}\:\mathrm{0}<{x}<\pi \\ $$

Commented by mnjuly1970 last updated on 03/Mar/21

$${peace}\:{be}\:{upon}\:{you}\: \\ $$$$\:\:{your}\:{effort}\:{really}\:{really}\:{admirable}\: \\ $$$$\:\:{i}\:{don}'{t}\:{know}\:{how}\:{old}\:{are}\:{you} \\ $$$${by}\:{the}\:{way}\:{your}\:{work}\:{is}\:{very} \\ $$$$\:\:{excellent}\:..{with}\:{the}\:{best}\:{wishes} \\ $$$$\:\:\:\:\:\:{allah}\:{keep}\:{you}…. \\ $$

Facebook Tweet Pin

sin1-sin2-2-sin3-3-sin4-4-1-2-

Leave a Reply Cancel reply