Menu Close

sinx-sin2x-sin3x-sinkx-sin-kx-2-sin-k-1-2-x-sin-x-2-prove-

Tinku Tara 0 Comments
Pin




Question Number 143439 by ERA last updated on 14/Jun/21
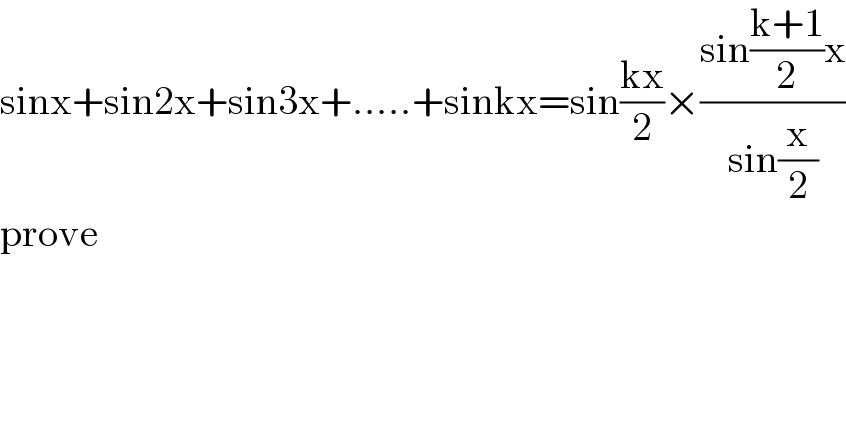
sinx+sin2x+sin3x+.....+sinkx=sin((kx)/2)×((sin((k+1)/2)x)/(sin(x/2))) prove
$$\mathrm{sinx}+\mathrm{sin2x}+\mathrm{sin3x}+…..+\mathrm{sinkx}=\mathrm{sin}\frac{\mathrm{kx}}{\mathrm{2}}×\frac{\mathrm{sin}\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}\mathrm{x}}{\mathrm{sin}\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$\mathrm{prove} \\ $$
Answered by Mathspace last updated on 14/Jun/21
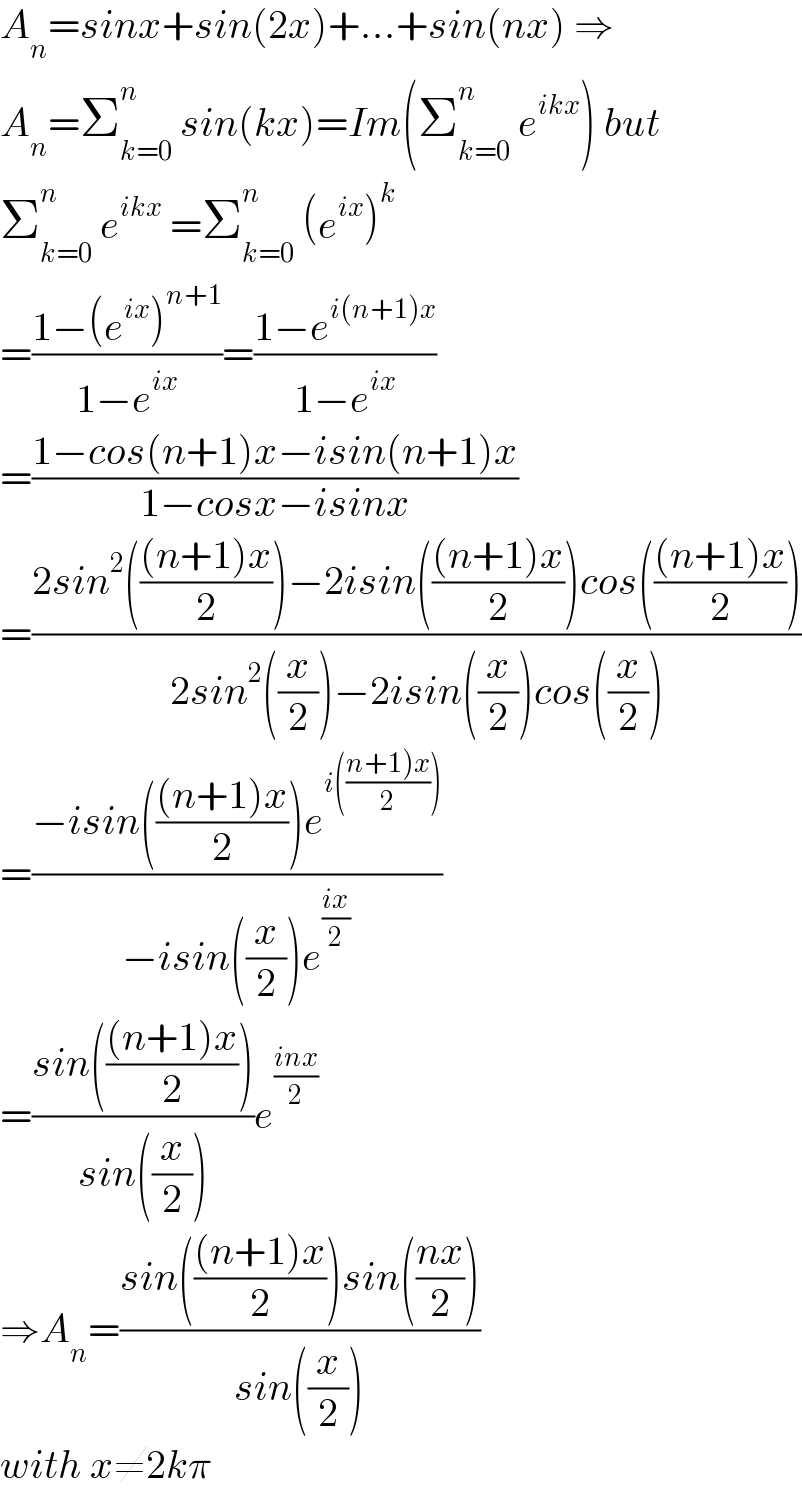
A_n =sinx+sin(2x)+...+sin(nx) ⇒ A_n =Σ_(k=0) ^n sin(kx)=Im(Σ_(k=0) ^n e^(ikx) ) but Σ_(k=0) ^n e^(ikx) =Σ_(k=0) ^n (e^(ix) )^k =((1−(e^(ix) )^(n+1) )/(1−e^(ix) ))=((1−e^(i(n+1)x) )/(1−e^(ix) )) =((1−cos(n+1)x−isin(n+1)x)/(1−cosx−isinx)) =((2sin^2 ((((n+1)x)/2))−2isin((((n+1)x)/2))cos((((n+1)x)/2)))/(2sin^2 ((x/2))−2isin((x/2))cos((x/2)))) =((−isin((((n+1)x)/2))e^(i(((n+1)x)/2))) )/(−isin((x/2))e^((ix)/2) )) =((sin((((n+1)x)/2)))/(sin((x/2))))e^((inx)/2) ⇒A_n =((sin((((n+1)x)/2))sin(((nx)/2)))/(sin((x/2)))) with x≠2kπ
$${A}_{{n}} ={sinx}+{sin}\left(\mathrm{2}{x}\right)+…+{sin}\left({nx}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{sin}\left({kx}\right)={Im}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{ikx}} \right)\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{e}^{{ikx}} \:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({e}^{{ix}} \right)^{{k}} \\ $$$$=\frac{\mathrm{1}−\left({e}^{{ix}} \right)^{{n}+\mathrm{1}} }{\mathrm{1}−{e}^{{ix}} }=\frac{\mathrm{1}−{e}^{{i}\left({n}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{ix}} } \\ $$$$=\frac{\mathrm{1}−{cos}\left({n}+\mathrm{1}\right){x}−{isin}\left({n}+\mathrm{1}\right){x}}{\mathrm{1}−{cosx}−{isinx}} \\ $$$$=\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)−\mathrm{2}{isin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right){cos}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{2}{isin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{−{isin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right){e}^{{i}\left(\frac{\left.{n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)} }{−{isin}\left(\frac{{x}}{\mathrm{2}}\right){e}^{\frac{{ix}}{\mathrm{2}}} } \\ $$$$=\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}{e}^{\frac{{inx}}{\mathrm{2}}} \\ $$$$\Rightarrow{A}_{{n}} =\frac{{sin}\left(\frac{\left({n}+\mathrm{1}\right){x}}{\mathrm{2}}\right){sin}\left(\frac{{nx}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$${with}\:{x}\neq\mathrm{2}{k}\pi \\ $$
Answered by gsk2684 last updated on 14/Jun/21
Σ_(t=1) ^k sin tx=imΣ_(t=1) ^k e^(itx) =imΣ_(t=1) ^k (e^(ix) )^t =im((e^(ix) ((e^(ix) )^k −1))/(e^(ix) −1)) =im((e^(i(k+1)x) −e^(ix) )/(e^(ix) −1)) =im{(e^(i(k+1)x) −e^(ix) )(e^(−ix) −1)/((cos x −1)^2 +sin^2 x)} =im((e^(ikx) −e^(i(k+1)x) −1+e^(ix) )/(2(1−cos x))) =(sin kx + sin x −sin (k+1)x)/(4 sin^2 (x/2)) =((2sin (((k+1)x)/2)cos(((k−1)x)/2)−2sin (((k+1)x)/2)cos (((k+1)x)/2))/(4sin^2 (x/2))) ={2sin (((k+1)x)/2).[cos(((kx)/2)−(x/2))−cos(((kx)/2)+(x/2))]}/4sin^2 (x/2) =((2sin (((k+1)x)/2).2sin ((kx)/2)sin (x/2))/(4sin^2 (x/2)))
$$\underset{\mathrm{t}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{sin}\:\mathrm{tx}=\mathrm{im}\underset{\mathrm{t}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{e}^{\mathrm{itx}} \\ $$$$=\mathrm{im}\underset{\mathrm{t}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{t}} \\ $$$$=\mathrm{im}\frac{\mathrm{e}^{\mathrm{ix}} \left(\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} −\mathrm{1}\right)}{\mathrm{e}^{\mathrm{ix}} −\mathrm{1}} \\ $$$$=\mathrm{im}\frac{\mathrm{e}^{\mathrm{i}\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}} −\mathrm{e}^{\mathrm{ix}} }{\mathrm{e}^{\mathrm{ix}} −\mathrm{1}} \\ $$$$=\mathrm{im}\left\{\left(\mathrm{e}^{\mathrm{i}\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}} −\mathrm{e}^{\mathrm{ix}} \right)\left(\mathrm{e}^{−\mathrm{ix}} −\mathrm{1}\right)/\left(\left(\mathrm{cos}\:\mathrm{x}\:−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\right\} \\ $$$$=\mathrm{im}\frac{\mathrm{e}^{\mathrm{ikx}} −\mathrm{e}^{\mathrm{i}\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}} −\mathrm{1}+\mathrm{e}^{\mathrm{ix}} }{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\left(\mathrm{sin}\:\mathrm{kx}\:+\:\mathrm{sin}\:\mathrm{x}\:−\mathrm{sin}\:\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}\right)/\left(\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\mathrm{x}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{2sin}\:\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}\mathrm{cos}\frac{\left(\mathrm{k}−\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}−\mathrm{2sin}\:\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}}{\mathrm{4sin}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$=\left\{\mathrm{2sin}\:\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}.\left[\mathrm{cos}\left(\frac{\mathrm{kx}}{\mathrm{2}}−\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{cos}\left(\frac{\mathrm{kx}}{\mathrm{2}}+\frac{\mathrm{x}}{\mathrm{2}}\right)\right]\right\}/\mathrm{4sin}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{2sin}\:\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}}.\mathrm{2sin}\:\frac{\mathrm{kx}}{\mathrm{2}}\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{4sin}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *