Question Number 9520 by ridwan balatif last updated on 12/Dec/16

$$\int\frac{\mathrm{sinxcosx}}{\mathrm{4}+\mathrm{sin}^{\mathrm{4}} \mathrm{x}}\mathrm{dx}=…? \\ $$
Answered by mrW last updated on 12/Dec/16
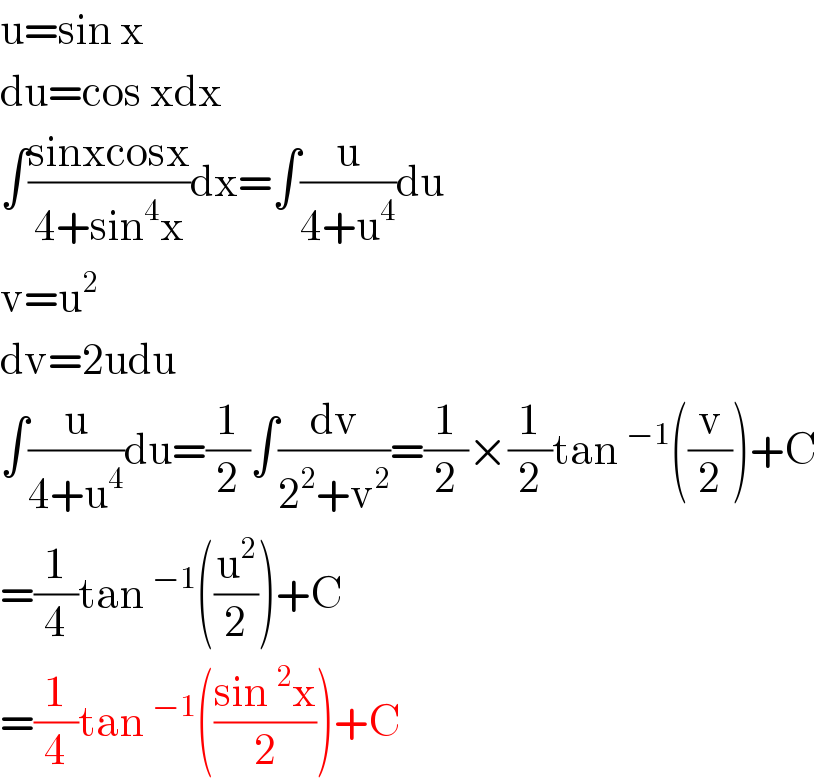
$$\mathrm{u}=\mathrm{sin}\:\mathrm{x} \\ $$$$\mathrm{du}=\mathrm{cos}\:\mathrm{xdx} \\ $$$$\int\frac{\mathrm{sinxcosx}}{\mathrm{4}+\mathrm{sin}^{\mathrm{4}} \mathrm{x}}\mathrm{dx}=\int\frac{\mathrm{u}}{\mathrm{4}+\mathrm{u}^{\mathrm{4}} }\mathrm{du} \\ $$$$\mathrm{v}=\mathrm{u}^{\mathrm{2}} \\ $$$$\mathrm{dv}=\mathrm{2udu} \\ $$$$\int\frac{\mathrm{u}}{\mathrm{4}+\mathrm{u}^{\mathrm{4}} }\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dv}}{\mathrm{2}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{\mathrm{v}}{\mathrm{2}}\right)+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{2}}\right)+\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{2}}\right)+\mathrm{C} \\ $$
Commented by ridwan balatif last updated on 12/Dec/16

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
