Question Number 131549 by liberty last updated on 06/Feb/21
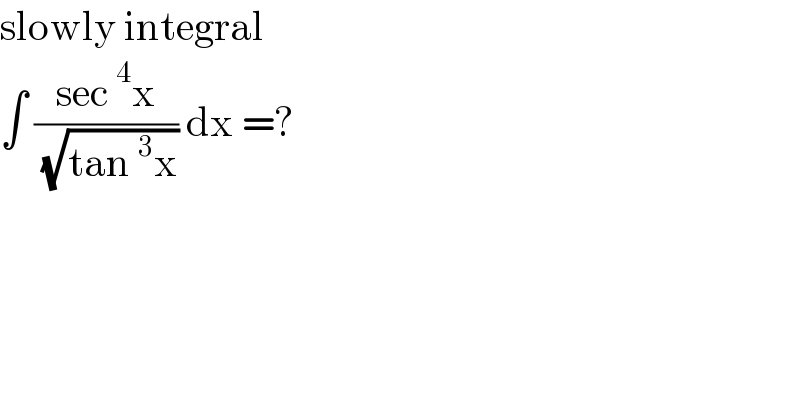
$$\mathrm{slowly}\:\mathrm{integral}\: \\ $$$$\int\:\frac{\mathrm{sec}\:^{\mathrm{4}} \mathrm{x}}{\:\sqrt{\mathrm{tan}\:^{\mathrm{3}} \mathrm{x}}}\:\mathrm{dx}\:=? \\ $$
Answered by rs4089 last updated on 06/Feb/21
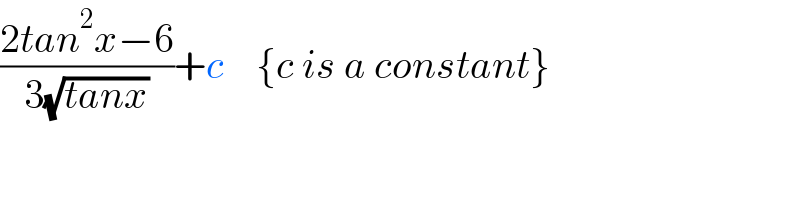
$$\frac{\mathrm{2}{tan}^{\mathrm{2}} {x}−\mathrm{6}}{\mathrm{3}\sqrt{{tanx}}}+{c}\:\:\:\:\left\{{c}\:{is}\:{a}\:{constant}\right\} \\ $$
Answered by EDWIN88 last updated on 06/Feb/21
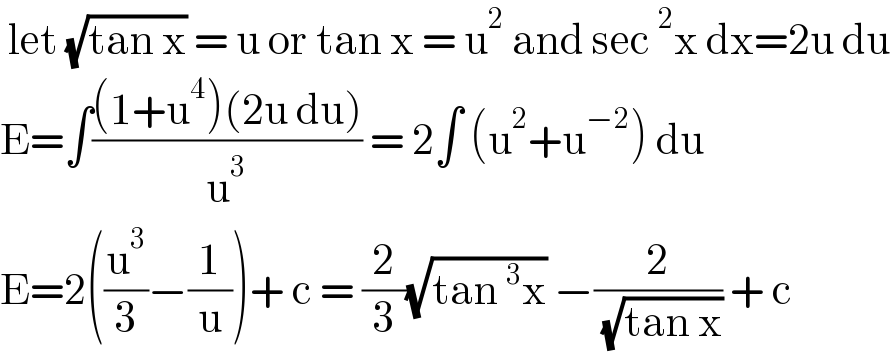
$$\:\mathrm{let}\:\sqrt{\mathrm{tan}\:\mathrm{x}}\:=\:\mathrm{u}\:\mathrm{or}\:\mathrm{tan}\:\mathrm{x}\:=\:\mathrm{u}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}=\mathrm{2u}\:\mathrm{du} \\ $$$$\mathrm{E}=\int\frac{\left(\mathrm{1}+\mathrm{u}^{\mathrm{4}} \right)\left(\mathrm{2u}\:\mathrm{du}\right)}{\mathrm{u}^{\mathrm{3}} }\:=\:\mathrm{2}\int\:\left(\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{−\mathrm{2}} \right)\:\mathrm{du} \\ $$$$\mathrm{E}=\mathrm{2}\left(\frac{\mathrm{u}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{u}}\right)+\:\mathrm{c}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{tan}\:^{\mathrm{3}} \mathrm{x}}\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{tan}\:\mathrm{x}}}\:+\:\mathrm{c} \\ $$
